【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: 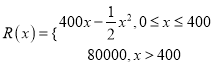 ,其中
,其中![]() 是仪器的月产量
是仪器的月产量
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数
的函数
(2)当月产量![]() 为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润)
参考答案:
【答案】(1) 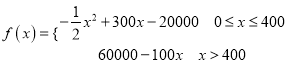 (2)当月产量为300台时,利润最大,最大利润是25000元.
(2)当月产量为300台时,利润最大,最大利润是25000元.
【解析】试题分析:(1);利润=总收益-总成本,而总成本包括固定成本20000元和生产![]() 台仪器所增加投入的
台仪器所增加投入的![]() 元;
元;
(2)根据上一问所列利润的分段函数,分别求每段函数的最大值,或是取值范围,再进行比较最大值,就是最大利润.
试题解析:(1)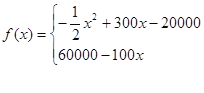
![]()
![]()
(2)当![]() 时,
时,
![]()
∴当![]() 时,
时,![]() 有最大值为
有最大值为![]()
当![]() 时,
时,
![]() 是减函数,
是减函数,
![]()
∴当![]() 时,
时,![]() 的最大值为
的最大值为![]()
答:每月生产![]() 台仪器时,利润最大,最大利润为
台仪器时,利润最大,最大利润为![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
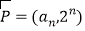 ,
,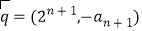 ,
,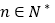 ,向量
,向量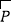 与
与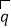 垂直,且
垂直,且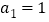 .
.(1)求数列
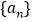 的通项公式;
的通项公式;(2)若数列
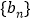 满足
满足 ,求数列
,求数列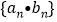 的前
的前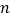 项和
项和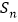 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
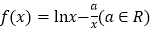 .
.(1)若函数
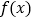 的图象在点
的图象在点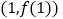 处的切线平行于直线
处的切线平行于直线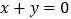 ,求
,求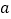 的值;
的值;(2)讨论函数
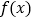 在定义域上的单调性;
在定义域上的单调性;(3)若函数
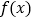 在
在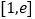 上的最小值为
上的最小值为 ,求
,求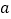 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(Ⅰ)应收集多少位女生样本数据?
(Ⅱ)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:
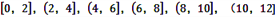 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率. 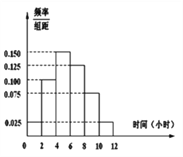
(Ⅲ)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有
 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.附:
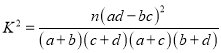
0.10
0.05
0.010
0.005
2.706
3.841
6.635
7.879
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)已知
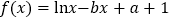
(1)求函数
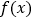 的单调区间;
的单调区间;(2)设
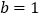 ,若存在
,若存在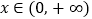 使得
使得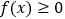 成立,求
成立,求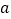 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发的一种药,如果成年人按规定的剂量服用,据监测,服药后每毫升中的含药量
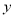 (微克)与时间
(微克)与时间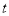 (小时)之间近似满足如图所示的曲线.(当
(小时)之间近似满足如图所示的曲线.(当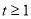 时,
时, 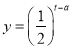 ).
).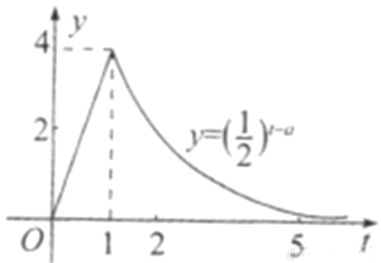
(1)写出第一次服药后
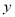 与
与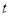 之间的函数关系式
之间的函数关系式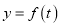 ;
;(2)据进一步测定,每毫升血液中含药量不少于
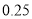 微克时,治疗疾病有效,求服药一次后治疗疾病有效时间.
微克时,治疗疾病有效,求服药一次后治疗疾病有效时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 定义在
定义在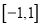 上的奇函数,
上的奇函数, 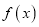 的最大值为
的最大值为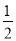 .
.(1)求函数
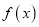 的解析式;
的解析式;(2)关于
 的方程
的方程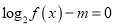 在
在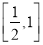 上有解,求实数
上有解,求实数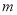 的取值范围;
的取值范围;(3)若存在
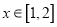 ,不等式
,不等式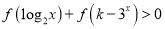 成立,请同学们探究实数
成立,请同学们探究实数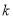 的所有可能取值.
的所有可能取值.
相关试题

