【题目】某地区不同身高的未成年男性的体重平均值如下表.
身高/ | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
体重/ | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 | 38.85 | 47.25 | 55.05 |
(1)根据表格提供的数据,能否建立恰当的函数模型,使它能比较近似地反映这个地区未成年男性体重![]() 与身高
与身高![]() 的函数关系?试写出这个函数模型的关系式.
的函数关系?试写出这个函数模型的关系式.
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为![]() ,体重为
,体重为![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考答案:
【答案】(1)![]() ;(2)这个男生偏胖.
;(2)这个男生偏胖.
【解析】
(1)画出散点图,考虑![]() 作为函数模型,代入数据计算得到答案.
作为函数模型,代入数据计算得到答案.
(2)根据函数解析式,代入数据![]() 得到
得到![]() ,计算得到答案.
,计算得到答案.
(1)以身高为横坐标,体重为纵坐标,画出散点图,
根据点的分布特征,可考虑以![]() 作为刻画这个地区未成年男性的体重与身高关系的函数模型.
作为刻画这个地区未成年男性的体重与身高关系的函数模型.

取其中的两组数据![]() ,
,![]() ,代入
,代入![]() 得:
得:
用计算器算得![]() ,
,![]() .
.
这样,我们就得到一个函数模型:![]() .
.
将已知数据代入上述函数关系式,或作出上述函数的图像,可以发现,这个函数模型与已知数据的拟合程度较好,这说明它能较好地反映这个地区未成年男性体重与身高的关系.
(2)将![]() 代入
代入![]() ,得
,得![]() ,由计算器算得
,由计算器算得![]() .
.
由于![]() ,所以,这个男生偏胖.
,所以,这个男生偏胖.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在空间四边形
 中,
中, ,
,
 ,
, ,
, ,且平面
,且平面 平面
平面 .
.
(1)求证:
 ;
;(2)若直线
 与平面
与平面 所成角的余弦值为
所成角的余弦值为 ,求
,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖励金额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:
 ,
, ,
, ,其中哪个模型能符合公司的要求?
,其中哪个模型能符合公司的要求? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆
 恒过点
恒过点 ,且与直线
,且与直线 相切.
相切.(1)求圆心
 的轨迹方程;
的轨迹方程;(2)若过点
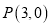 的直线交轨迹
的直线交轨迹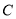 于
于 ,
,  两点,直线
两点,直线 ,
,  (
( 为坐标原点)分别交直线
为坐标原点)分别交直线 于点
于点 ,
,  ,证明:以
,证明:以 为直径的圆被
为直径的圆被 轴截得的弦长为定值.
轴截得的弦长为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(1)若对于任意的
 ,
,  恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)若
 ,设函数
,设函数 在区间
在区间 上的最大值、最小值分别为
上的最大值、最小值分别为 、
、 ,记
,记 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
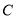 的方程为:
的方程为: .
.(1)直线
 过点
过点 ,且与圆
,且与圆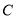 交于
交于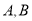 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;(2)圆
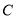 上有一动点
上有一动点 ,
, ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,已知直线
中,已知直线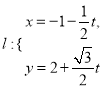 (
( 为参数),曲线
为参数),曲线 (
( 为参数),以原点
为参数),以原点 为极点,
为极点,  轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.(1)写出直线
 的普通方程与曲线
的普通方程与曲线 的极坐标方程;
的极坐标方程;(2)设直线
 与曲线
与曲线 交于
交于 ,
,  两点,求
两点,求 的面积.
的面积.
相关试题

