【题目】已知圆![]() 与圆
与圆![]() ,点
,点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 上.
上.
(1)求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 由无数对相互垂直的直线
由无数对相互垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() 满足题意
满足题意
【解析】试题分析:(1)根据圆的几何条件可得![]() 为两圆心连线与两圆交点时最小,再根据两点间距离公式计算结果(2)两弦长相等转化为对应圆心距相等,根据点到直线距离公式展开得关于斜率k的恒等式,再根据恒等式成立的条件解出点
为两圆心连线与两圆交点时最小,再根据两点间距离公式计算结果(2)两弦长相等转化为对应圆心距相等,根据点到直线距离公式展开得关于斜率k的恒等式,再根据恒等式成立的条件解出点![]() 坐标
坐标
试题解析:(1)![]() 为两圆心连线与两圆交点时最小,此时
为两圆心连线与两圆交点时最小,此时![]()
(2)设![]() ,斜率不存在时不符合题意,舍去;斜率存在时,则
,斜率不存在时不符合题意,舍去;斜率存在时,则![]() 即
即![]() ,
, ![]() 即
即![]() ,
, ![]()
由题意可知,两弦长相等也就是![]() 和
和![]() 相等即可,故
相等即可,故![]() 即
即![]() ,化简得:
,化简得: ![]() 对任意
对任意![]() 恒成立,故
恒成立,故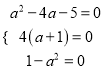 ,解得
,解得![]() ,故存在点
,故存在点![]() 满足题意.
满足题意.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中常数
,其中常数 .
.(1)当
 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;(2)设定义在
 上的函数
上的函数 在点
在点 处的切线方程为
处的切线方程为 ,若
,若 在
在 内恒成立,则称
内恒成立,则称 为函数
为函数 的“类对称点”,当
的“类对称点”,当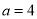 时,试问
时,试问 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:方程
 表示焦点在x轴上的椭圆;命题q:双曲线
表示焦点在x轴上的椭圆;命题q:双曲线 的离心率e∈
的离心率e∈ .若命题“p∨q”为真命题,“p∧q”为假命题,求m的取值范围.
.若命题“p∨q”为真命题,“p∧q”为假命题,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列
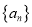 的前
的前 项和为
项和为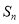 ,已知
,已知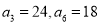 .
.(1)求数列
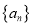 的通项公式;
的通项公式;(2)求数列
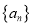 的前
的前 项和为
项和为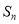 ;
;(3)当
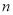 为何值时,
为何值时, 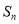 最大,并求
最大,并求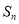 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣
 +x在区间[m,n]上的最小值是2m,最大值是2n,求m,n的值.
+x在区间[m,n]上的最小值是2m,最大值是2n,求m,n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
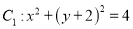 与圆
与圆
(1)若直线
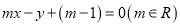 与圆
与圆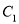 相交于
相交于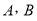 两个不同点,求
两个不同点,求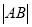 的最小值;
的最小值;(2)直线
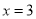 上是否存在点
上是否存在点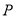 ,满足经过点
,满足经过点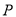 有无数对互相垂直的直线
有无数对互相垂直的直线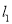 和
和 ,它们分别与圆
,它们分别与圆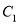 和圆
和圆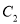 相交,并且直线
相交,并且直线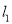 被圆
被圆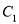 所截得的弦长等于直线
所截得的弦长等于直线 被圆
被圆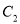 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N,数列{bn}满足an=4log2bn+3,n∈N.
(1)求an,bn;
(2)求数列{anbn}的前n项和Tn.
相关试题

