【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,其中
为平行四边形,其中![]() ,
,![]() ,
,![]() ,等边
,等边![]() 所在平面与平面
所在平面与平面![]() 垂直.
垂直.
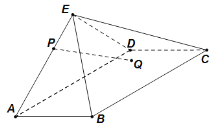
(Ⅰ)点![]() 在棱
在棱![]() 上,且
上,且![]() ,
,![]() 为
为![]() 的重心,求证:
的重心,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】见解析
【解析】(Ⅰ)如图,在棱![]() 上取点
上取点![]() ,使得
,使得![]() ;连接
;连接![]() 并延长,交
并延长,交![]() 于点
于点![]() .
.
因为在![]() 中,
中,![]() ,所以
,所以![]() ,
,
又四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
所以![]() . -----------------2分
. -----------------2分
在![]() 中,
中,![]() 为重心,所以
为重心,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() . ---------5分
. ---------5分
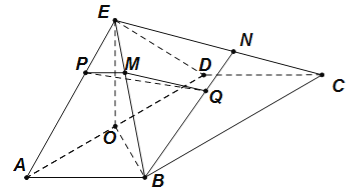
(Ⅱ)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() 的面积
的面积![]() .--7分
.--7分
取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() ,且
,且![]() .
.
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .--------------10分
.--------------10分
故三棱锥![]() 的体积
的体积![]() .-------12分
.-------12分
【命题意图】本题考查空间中线面平行的证明、几何体体积的求解,考查基本的空间想象能力和逻辑推理能力、运算能力等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
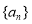 的前
的前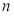 项和为
项和为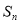 ,
,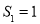 ,
,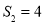 ,且当
,且当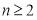 时,
时,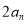 与6的等差中项为
与6的等差中项为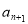 .数列
.数列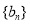 为等比数列,且
为等比数列,且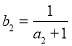 ,
,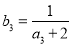 .
.(Ⅰ)求数列
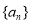 、
、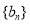 的通项公式;
的通项公式;(Ⅱ)求数列
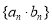 的前
的前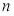 项和
项和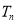 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
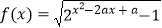 的定义域为R,则实数a的取值范围是 .
的定义域为R,则实数a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设锐角三角形
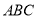 的内角
的内角 的对边分别为
的对边分别为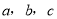 ,
, 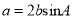 .
.(Ⅰ)求
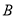 的大小;
的大小;(Ⅱ)求
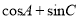 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意实数x,[x]表示不超过x的最大整数,如[1.1]=1,[﹣2.1]=﹣3.定义在R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0<x<1},则A中所有元素之和为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
已知直线l经过点
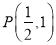 ,倾斜角
,倾斜角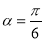 ,圆
,圆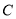 的极坐标方程为
的极坐标方程为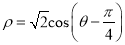 .
.(Ⅰ)写出直线l的参数方程,并把圆
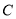 的方程化为直角坐标方程;
的方程化为直角坐标方程;(Ⅱ)设l与圆
 相交于
相交于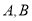 两点,求点
两点,求点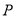 到
到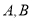 两点的距离之积.
两点的距离之积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
相关试题

