【题目】如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2![]() , AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
, AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
参考答案:
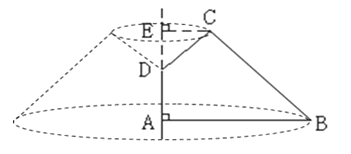
【答案】解:四边形ABCD绕AD旋转一周所成的
几何体,如右图:
S表面=S圆台下底面+S圆台侧面+S圆锥侧面
=πr22+π(r1+r2)l2+πr1l1
=![]()
=25π+35π+4![]() π
π
=60π+4![]() π.
π.
体积V=V圆台﹣V圆锥
=![]() [25π+
[25π+![]() +4π]×4﹣
+4π]×4﹣![]() ×2π×2×2
×2π×2×2
=![]() ×39π×4﹣
×39π×4﹣![]() ×8π
×8π
=![]() .
.
所求表面积为:60π+4![]() π,体积为:
π,体积为:![]() .
.
【解析】旋转后的几何体是圆台除去一个倒放的圆锥,根据题目所给数据,求出圆台的侧面积、圆锥的侧面积、圆台的底面积,即可求出几何体的表面积.求出圆台体积减去圆锥体积,即可得到几何体的体积.
-
科目: 来源: 题型:
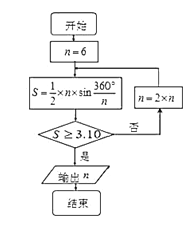
查看答案和解析>>【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值
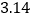 ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出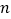 的值为 ( )
的值为 ( )(参考数据:
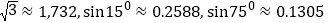 )
)
A.
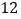 B.
B. 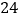 C.
C. 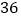 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点C(t,
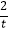 ) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
) (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y﹣4=0与圆C交于点M、N,若OM=ON,求圆C的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是正四棱柱
是正四棱柱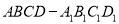 的一个截面,此截面与棱
的一个截面,此截面与棱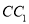 交于点
交于点 ,
, 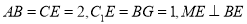 ,其中
,其中 分别为棱
分别为棱 上一点.
上一点.(1)证明:平面
 平面
平面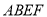 ;
;(2)
 为线段
为线段 上一点,若四面体
上一点,若四面体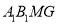 与四棱锥
与四棱锥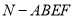 的体积相等,求
的体积相等,求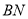 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
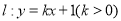 关于直线
关于直线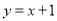 对称的直线为
对称的直线为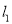 ,直线
,直线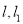 与椭圆
与椭圆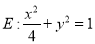 分别交于点
分别交于点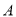 、
、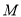 和
和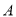 、
、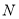 ,记直线
,记直线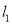 的斜率为
的斜率为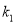 .
.(Ⅰ)求
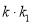 的值;
的值;(Ⅱ)当
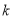 变化时,试问直线
变化时,试问直线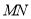 是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
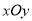 中,已知椭圆
中,已知椭圆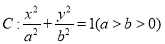 的离心率为
的离心率为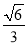 ,且过点
,且过点 .
.(1)求
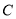 的方程;
的方程;(2)若动点
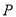 在直线
在直线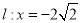 上,过
上,过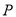 作直线交椭圆
作直线交椭圆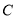 于
于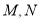 两点,使得
两点,使得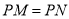 ,再过
,再过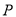 作直线
作直线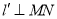 ,证明:直线
,证明:直线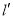 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点到准线的距离为
的焦点到准线的距离为 ,直线
,直线 与抛物线
与抛物线 交于
交于 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点 .
.(1)若
 的坐标为
的坐标为 ,求
,求 的值;
的值;(2)设线段
 的中点为
的中点为 ,点
,点 的坐标为
的坐标为 ,过
,过 的直线
的直线 与线段
与线段 为直径的圆相切,切点为
为直径的圆相切,切点为 ,且直线
,且直线 与抛物线
与抛物线 交于
交于 两点,求
两点,求 的取值范围.
的取值范围.
相关试题

