【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
参考答案:
【答案】(1)![]() (2)
(2)
【解析】试题分析:
(1)由题意得![]() ,根据离心率为
,根据离心率为![]() 可得
可得![]() ,故可得到C的方程。(2)由
,故可得到C的方程。(2)由![]() 为线段
为线段![]() 的中点。设
的中点。设 ,当
,当![]() 时,由“点差法”可得直线
时,由“点差法”可得直线![]() 的斜率为
的斜率为![]() ,从而直线
,从而直线![]() 的方程可求得为
的方程可求得为![]()
,过定点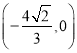 ;当
;当![]() 时,
时, ![]() 过点
过点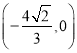 。故可得直线
。故可得直线![]() 过点
过点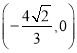 。
。
试题解析:
(1)由题意知![]() ,
,
又椭圆的离心率为![]() ,所以
,所以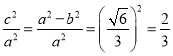 ,
,
所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)因为直线![]() 的方程为
的方程为![]() ,设
,设 ,
,
①当![]() 时,设
时,设![]() ,显然
,显然![]() ,
,
由 可得
可得![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() 为线段
为线段![]() 的中点,
的中点,
故直线![]() 的斜率为
的斜率为![]() ,
,
又![]() ,
,
所以直线![]() 的方程为
的方程为![]()
即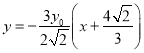 ,显然
,显然![]() 恒过定点
恒过定点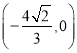 ,
,
②当![]() 时,
时, ![]() 过点
过点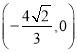 ,
,
综上可得直线![]() 过定点
过定点 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是正四棱柱
是正四棱柱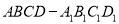 的一个截面,此截面与棱
的一个截面,此截面与棱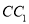 交于点
交于点 ,
, 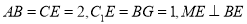 ,其中
,其中 分别为棱
分别为棱 上一点.
上一点.(1)证明:平面
 平面
平面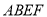 ;
;(2)
 为线段
为线段 上一点,若四面体
上一点,若四面体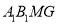 与四棱锥
与四棱锥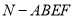 的体积相等,求
的体积相等,求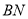 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2
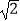 , AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
, AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
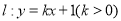 关于直线
关于直线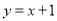 对称的直线为
对称的直线为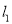 ,直线
,直线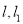 与椭圆
与椭圆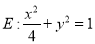 分别交于点
分别交于点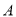 、
、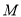 和
和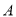 、
、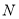 ,记直线
,记直线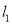 的斜率为
的斜率为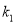 .
.(Ⅰ)求
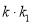 的值;
的值;(Ⅱ)当
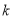 变化时,试问直线
变化时,试问直线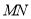 是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点到准线的距离为
的焦点到准线的距离为 ,直线
,直线 与抛物线
与抛物线 交于
交于 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点 .
.(1)若
 的坐标为
的坐标为 ,求
,求 的值;
的值;(2)设线段
 的中点为
的中点为 ,点
,点 的坐标为
的坐标为 ,过
,过 的直线
的直线 与线段
与线段 为直径的圆相切,切点为
为直径的圆相切,切点为 ,且直线
,且直线 与抛物线
与抛物线 交于
交于 两点,求
两点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.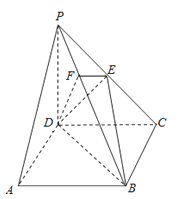
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
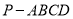 的底面
的底面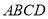 为平行四边形,平面
为平行四边形,平面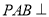 平面
平面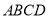 ,
, 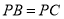 ,
,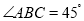 .
.(Ⅰ)求证:
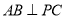 ;
;(Ⅱ)若三角形
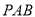 是边长为
是边长为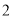 的等边三角形,求三棱锥
的等边三角形,求三棱锥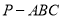 外接球的表面积.
外接球的表面积. 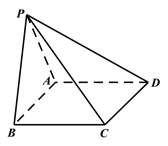
相关试题

