【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3
的等比数列,设bn+2=3 ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() +m﹣1对一切正整数n恒成立,求实数m的取值范围.
+m﹣1对一切正整数n恒成立,求实数m的取值范围.
参考答案:
【答案】
(1)证明:由题意知,an=( ![]() )n.
)n.
∵ ![]() ,
, ![]()
∴b1=1
∴bn+1﹣bn=3 ![]() an+1﹣3
an+1﹣3 ![]() an=3
an=3 ![]()
![]() =3
=3 ![]() q=3
q=3
∴数列{bn}是首项为1,公差为3的等差数列
(2)解:由(1)知,an=( ![]() )n.bn=3n﹣2
)n.bn=3n﹣2
∴Cn=(3n﹣2)×( ![]() )n.
)n.
∴Sn=1× ![]() +4×(
+4×( ![]() )2+…+(3n﹣2)×(
)2+…+(3n﹣2)×( ![]() )n,
)n,
于是 ![]() Sn=1×(
Sn=1×( ![]() )2+4×(
)2+4×( ![]() )3+…(3n﹣2)×(
)3+…(3n﹣2)×( ![]() )n+1,
)n+1,
两式相减得 ![]() Sn=
Sn= ![]() +3×[(
+3×[( ![]() )2+(
)2+( ![]() )3+…+(
)3+…+( ![]() )n)﹣(3n﹣2)×(
)n)﹣(3n﹣2)×( ![]() )n+1,
)n+1,
= ![]() ﹣(3n+2)×(
﹣(3n+2)×( ![]() )n+1,
)n+1,
∴Sn= ![]() ﹣
﹣ ![]() (
( ![]() )n
)n
(3)解:∵Cn+1﹣Cn=(3n+1)×( ![]() )n+1﹣(3n﹣2)×(
)n+1﹣(3n﹣2)×( ![]() )n=9(1﹣n)×(
)n=9(1﹣n)×( ![]() )n+1,
)n+1,
∴当n=1时,C2=C1= ![]()
当n≥2时,Cn+1<Cn,即C2=C1>C3>C4>…>Cn
∴当n=1时,Cn取最大值是 ![]()
又 ![]()
∴ ![]() ≥
≥ ![]()
即m2+4m﹣5≥0解得m≥1或m≤﹣5
【解析】(1)根据等比数列的通项公式可求得an , 代入 ![]() 求得bn+1﹣bn为常数,进而判断出数列{bn}是等差数列.(2)由(1)可分别求得an和bn , 进而求得Cn进而用错位相减法进行求和.(3)把(2)中的Cn , 代入Cn+1﹣Cn结果小于0,进而判断出当n≥2时,Cn+1<Cn , 进而可推断出当n=1时,Cn取最大值,问题转化为
求得bn+1﹣bn为常数,进而判断出数列{bn}是等差数列.(2)由(1)可分别求得an和bn , 进而求得Cn进而用错位相减法进行求和.(3)把(2)中的Cn , 代入Cn+1﹣Cn结果小于0,进而判断出当n≥2时,Cn+1<Cn , 进而可推断出当n=1时,Cn取最大值,问题转化为 ![]() ≥
≥ ![]() ,求得m的取值范围.
,求得m的取值范围.
【考点精析】本题主要考查了等差关系的确定和数列的前n项和的相关知识点,需要掌握如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系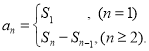 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆
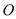 的圆心与矩形
的圆心与矩形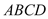 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(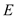 为上切点),与左右两边相交(
为上切点),与左右两边相交(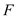 ,
, 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1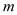 ,且
,且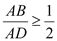 ,设
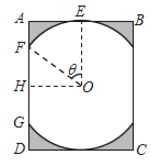
,设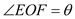 ,透光区域的面积为
,透光区域的面积为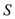 .
.
(1)求
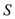 关于
关于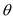 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边
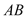 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,点
中,点 ,直线
,直线 与动直线
与动直线 的交点为
的交点为 ,线段
,线段 的中垂线与动直线
的中垂线与动直线 的交点为
的交点为 .
.
(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)过动点
 作曲线
作曲线 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,求证:
,求证: 的大小为定值.
的大小为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个无穷数列
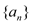 和
和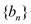 的前
的前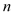 项和分别为
项和分别为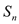 ,
,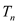 ,
,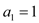 ,
,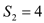 ,对任意的
,对任意的 ,都有
,都有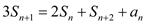 .
.(1)求数列
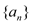 的通项公式;
的通项公式;(2)若
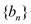 为等差数列,对任意的
为等差数列,对任意的 ,都有
,都有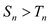 .证明:
.证明: ;
;(3)若
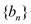 为等比数列,
为等比数列, ,
,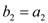 ,求满足
,求满足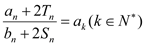 的
的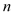 值.
值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知集合

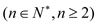 ,对于集合
,对于集合 的两个非空子集
的两个非空子集 ,
, ,若
,若 ,则称
,则称 为集合
为集合 的一组“互斥子集”.记集合
的一组“互斥子集”.记集合 的所有“互斥子集”的组数为
的所有“互斥子集”的组数为 (视
(视 与
与 为同一组“互斥子集”).
为同一组“互斥子集”).(1)写出
 ,
, ,
, 的值;
的值;(2)求
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________________元.
相关试题

