【题目】选修4-5:不等式选讲
已知集合![]()
![]() ,对于集合
,对于集合![]() 的两个非空子集
的两个非空子集![]() ,
,![]() ,若
,若![]() ,则称
,则称![]() 为集合
为集合![]() 的一组“互斥子集”.记集合
的一组“互斥子集”.记集合![]() 的所有“互斥子集”的组数为
的所有“互斥子集”的组数为![]() (视
(视![]() 与
与![]() 为同一组“互斥子集”).
为同一组“互斥子集”).
(1)写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() .
.
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() .
.
(2)见解析
【解析】试题分析:
(1)由新定义的知识可得![]() ;
;
(2) 设集合![]() 中有
中有![]() 个元素,
个元素,![]() .
.
则与集合![]() 互斥的非空子集有
互斥的非空子集有![]() 个.
个.
结合组合数的性质计算可得![]() .
.
试题解析:
解:(1) ![]() ,
,![]() ,
,
![]() .
.
(2)解法一:设集合![]() 中有
中有![]() 个元素,
个元素,![]() .
.
则与集合![]() 互斥的非空子集有
互斥的非空子集有![]() 个.
个.
于是![]()
![]() .
.
因为![]()
![]()
![]() ,
,
![]()
![]() ,
,
所以![]()
![]() .
.
解法二:任意一个元素只能在集合![]() ,
,![]() ,
,![]() 之一中,
之一中,
则这![]() 个元素在集合
个元素在集合![]() ,
,![]() ,
,![]() 中,共有
中,共有![]() 种;
种;
其中![]() 为空集的种数为
为空集的种数为![]() ,
,![]() 为空集的种数为
为空集的种数为![]() ,
,
所以![]() ,
,![]() 均为非空子集的种数为
均为非空子集的种数为![]() ,
,
又![]() 与
与![]() 为同一组“互斥子集”,
为同一组“互斥子集”,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,点
中,点 ,直线
,直线 与动直线
与动直线 的交点为
的交点为 ,线段
,线段 的中垂线与动直线
的中垂线与动直线 的交点为
的交点为 .
.
(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)过动点
 作曲线
作曲线 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,求证:
,求证: 的大小为定值.
的大小为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是首项为a1=
 ,公比q=
,公比q=  的等比数列,设bn+2=3
的等比数列,设bn+2=3  an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤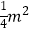 +m﹣1对一切正整数n恒成立,求实数m的取值范围.
+m﹣1对一切正整数n恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个无穷数列
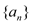 和
和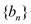 的前
的前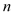 项和分别为
项和分别为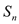 ,
,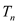 ,
,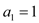 ,
,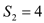 ,对任意的
,对任意的 ,都有
,都有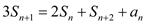 .
.(1)求数列
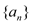 的通项公式;
的通项公式;(2)若
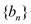 为等差数列,对任意的
为等差数列,对任意的 ,都有
,都有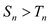 .证明:
.证明: ;
;(3)若
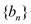 为等比数列,
为等比数列, ,
,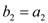 ,求满足
,求满足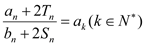 的
的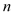 值.
值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)
(2017天津)电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧播放时长(分钟)
广告播放时长(分钟)
收视人次(万)
甲
70
5
60
乙
60
5
25
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用
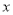 ,
,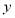 表示每周计划播出的甲、乙两套连续剧的次数.
表示每周计划播出的甲、乙两套连续剧的次数.(1)用
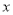 ,
,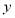 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若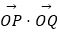 =﹣2,求实数k的值;
=﹣2,求实数k的值;
(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
相关试题

