【题目】某手机生产企业为了解消费者对某款手机功能的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有30份给予回复,这30份的评分如下:

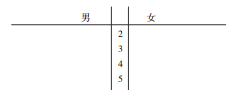
(Ⅰ)完成下面的茎叶图,并求16名男消费者评分的中位数与14名女消费者评分的平均值;

(Ⅱ)若大于40分为“满意”,否则为“不满意”,完成上面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费者对该款手机的“满意度”与性别有关.
的把握认为消费者对该款手机的“满意度”与性别有关.
参考公式:  ,其中
,其中![]()
参考数据:

参考答案:
【答案】(1)见解析(2)没有![]() 的把握
的把握
【解析】试题分析:(Ⅰ)由茎叶图可得到16名男消费者的中位数,同理可求出女消费者评分的平均值,根据所给的数据可得列联表;(Ⅱ)根据列联表求出, ![]()
![]() ,所以没有
,所以没有![]() 的把握认为消费者对该款手机的“满意度”与性别有关.
的把握认为消费者对该款手机的“满意度”与性别有关.
试题解析:
(Ⅰ)茎叶图如图.

由图可知男消费者评分的中位数是45.5,
女消费者评分的平均值为![]()
![]()
![]()
![]() .
.

(Ⅱ)列联表如图, ![]()
![]() ,所以没有
,所以没有![]() 的把握认为消费者对该款手机的“满意度”与性别有关.
的把握认为消费者对该款手机的“满意度”与性别有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点
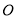 为极点,
为极点, 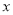 轴的正半轴为极轴建立坐标系,已知点
轴的正半轴为极轴建立坐标系,已知点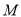 的直角坐标为
的直角坐标为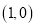 ,若直线
,若直线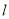 的极坐标方程为
的极坐标方程为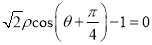 .曲线
.曲线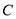 的参数方程是
的参数方程是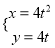 (
(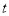 为参数).
为参数).(1)求直线
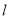 和曲线
和曲线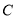 的普通方程;
的普通方程;(2)设直线
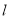 和曲线
和曲线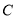 交于
交于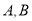 两点,求
两点,求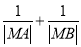 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,给当地人民造成了巨大的财产损失,适逢暑假,小张调查了当地某小区的100户居民由于台风造成的经济损失,将收集的数据分成
 ,
,  ,
,  ,
,  ,
,  五组,并作出如下频率分布直方图(图1):
五组,并作出如下频率分布直方图(图1):(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如右下表格,在图2表格空白处填写正确数字,并说明是否有
 以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?

(Ⅱ)将上述调查所得到的频率视为概率. 现在从该地区大量受灾居民中,采用随机抽样方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为
 . 若每次抽取的结果是相互独立的,求
. 若每次抽取的结果是相互独立的,求 的分布列,期望
的分布列,期望 和方差
和方差 .
.附:临界值表

0.10
0.05
0.025

2.706
3.841
5.024
随机量变

-
科目: 来源: 题型:
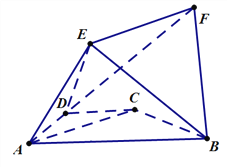
查看答案和解析>>【题目】如图,在梯形
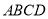 中,
中, 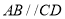 ,
, 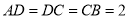 ,
, 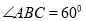 ,平面
,平面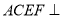 平面
平面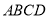 ,四边形
,四边形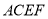 是菱形,
是菱形, 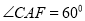 .
.
(1)求证:
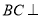 平面
平面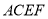 ;
;(2)求平面
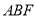 与平面
与平面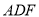 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 和点
和点 ,动圆
,动圆 经过点
经过点 且与圆
且与圆 相切,圆心
相切,圆心 的轨迹为曲线
的轨迹为曲线
(1)求曲线
 的方程;
的方程;(2)点
 是曲线
是曲线 与
与 轴正半轴的交点,点
轴正半轴的交点,点 在曲线
在曲线 上,若直线
上,若直线 的斜率
的斜率 满足
满足 求
求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有
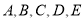 五辆汽车,其中
五辆汽车,其中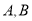 两辆汽车的车牌尾号均为1.
两辆汽车的车牌尾号均为1. 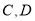 两辆汽车的车牌尾号均为2,
两辆汽车的车牌尾号均为2, 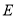 车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车,
车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车, 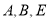 三辆汽车每天出车的概率均为
三辆汽车每天出车的概率均为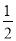 ,
, 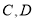 两辆汽车每天出车的概率均为
两辆汽车每天出车的概率均为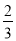 ,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:车牌尾号
0和5
1和6
2和7
3和8
4和9
限行日
星期一
星期二
星期三
星期四
星期五
(1)求该公司在星期一至少有2辆汽车出国的概率;
(2)设
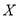 表示该公司在星期二和星期三两天出车的车辆数之和,求
表示该公司在星期二和星期三两天出车的车辆数之和,求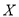 的分布列及期望.
的分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  (
( )的焦距为
)的焦距为 ,点
,点 在
在 上.
上.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设点
 在
在 上,点
上,点 的轨迹为曲线
的轨迹为曲线 ,过原点作直线
,过原点作直线 与曲线
与曲线 交于
交于 、
、 两点,点
两点,点 ,证明:
,证明:  为定值,并求出定值.
为定值,并求出定值.
相关试题

