【题目】已知椭圆![]() :
: ![]() (
(![]() )的焦距为
)的焦距为![]() ,点
,点 在
在![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设点![]() 在
在![]() 上,点
上,点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过原点作直线
,过原点作直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() ,证明:
,证明: ![]() 为定值,并求出定值.
为定值,并求出定值.
参考答案:
【答案】(1)![]() (2)3
(2)3
【解析】试题分析:(Ⅰ)由题意知:c=![]() ,根据椭圆定义可求得a,根据b2=a2-c2可得b;(Ⅱ)分直线
,根据椭圆定义可求得a,根据b2=a2-c2可得b;(Ⅱ)分直线![]() 的斜率为0,不为0两种情况进行讨论:当直线
的斜率为0,不为0两种情况进行讨论:当直线![]() 的斜率为0时直接按照向量数量积运算即可;当直线
的斜率为0时直接按照向量数量积运算即可;当直线![]() 的斜率不为0时,设直线
的斜率不为0时,设直线![]() 的方程为:
的方程为: ![]() ,
, ![]() ,
, ![]() .联立直线方程与椭圆方程消掉y得x的一元二次方程,由韦达定理及向量数量积公式代入运算可得结论;
.联立直线方程与椭圆方程消掉y得x的一元二次方程,由韦达定理及向量数量积公式代入运算可得结论;
试题解析:
(Ⅰ)由已知得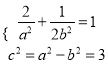 ,解得
,解得![]() ,
, ![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)由条件可得![]() ,
, ![]() 曲线
曲线![]() 的方程为
的方程为![]() .
.
当直线![]() 的斜率不存在时,不妨设
的斜率不存在时,不妨设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ;
;
当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,可设点
,可设点![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
把点![]() 代入曲线
代入曲线![]() 的方程
的方程![]() 得
得![]() ,
, ![]() .
.
综上可知, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机生产企业为了解消费者对某款手机功能的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有30份给予回复,这30份的评分如下:

(Ⅰ)完成下面的茎叶图,并求16名男消费者评分的中位数与14名女消费者评分的平均值;
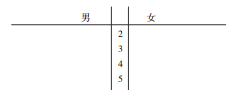

(Ⅱ)若大于40分为“满意”,否则为“不满意”,完成上面的
 列联表,并判断是否有
列联表,并判断是否有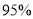 的把握认为消费者对该款手机的“满意度”与性别有关.
的把握认为消费者对该款手机的“满意度”与性别有关.参考公式:
 ,其中
,其中
参考数据:

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 和点
和点 ,动圆
,动圆 经过点
经过点 且与圆
且与圆 相切,圆心
相切,圆心 的轨迹为曲线
的轨迹为曲线
(1)求曲线
 的方程;
的方程;(2)点
 是曲线
是曲线 与
与 轴正半轴的交点,点
轴正半轴的交点,点 在曲线
在曲线 上,若直线
上,若直线 的斜率
的斜率 满足
满足 求
求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有
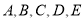 五辆汽车,其中
五辆汽车,其中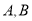 两辆汽车的车牌尾号均为1.
两辆汽车的车牌尾号均为1. 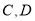 两辆汽车的车牌尾号均为2,
两辆汽车的车牌尾号均为2, 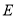 车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车,
车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车, 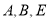 三辆汽车每天出车的概率均为
三辆汽车每天出车的概率均为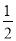 ,
, 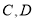 两辆汽车每天出车的概率均为
两辆汽车每天出车的概率均为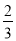 ,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:车牌尾号
0和5
1和6
2和7
3和8
4和9
限行日
星期一
星期二
星期三
星期四
星期五
(1)求该公司在星期一至少有2辆汽车出国的概率;
(2)设
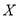 表示该公司在星期二和星期三两天出车的车辆数之和,求
表示该公司在星期二和星期三两天出车的车辆数之和,求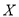 的分布列及期望.
的分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE,D1F,DA三线交于一点.
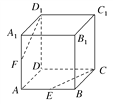
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是__________.(写出所有正确命题的序号)
①已知
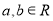 ,“
,“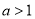 且
且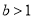 ”是“
”是“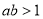 ”的充要条件;
”的充要条件;②已知平面向量
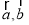 ,“
,“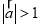 且
且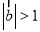 ”是“
”是“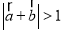 ”的必要不充分条件;
”的必要不充分条件;③已知
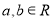 ,“
,“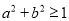 ”是“
”是“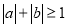 ”的充分不必要条件;
”的充分不必要条件;④命题
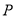 :“
:“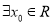 ,使
,使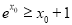 且
且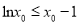 ”的否定为
”的否定为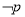 :“
:“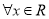 ,都有
,都有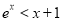 且
且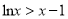 ”
” -
科目: 来源: 题型:
查看答案和解析>>【题目】已知焦点在
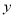 轴上的椭圆
轴上的椭圆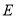 的中心是原点
的中心是原点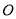 ,离心率为双曲线
,离心率为双曲线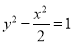 离心率的一半,直线
离心率的一半,直线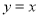 被椭圆
被椭圆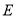 截得的线段长为
截得的线段长为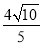 .直线
.直线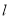 :
: 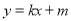 与
与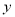 轴交于点
轴交于点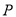 ,与椭圆
,与椭圆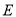 交于
交于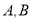 两个相异点,且
两个相异点,且 .
.(1)求椭圆
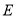 的方程;
的方程;(2)是否存在实数
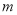 ,使
,使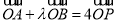 ?若存在,求
?若存在,求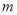 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
相关试题

