【题目】一个袋子里装有7个球,其中有红球4个,编号分别为1,2,3,4;白球3个,编号分别为2,3,4.从袋子中任取4个球(假设取到任何一个球的可能性相同).
(Ⅰ)求取出的4个球中,含有编号为3的球的概率;
(Ⅱ)在取出的4个球中,红球编号的最大值设为X,求随机变量X的分布列和数学期望.
参考答案:
【答案】解:(Ⅰ)设“取出的4个球中,含有编号为3的球”为事件A,则 ![]()
所以,取出的4个球中,含有编号为3的球的概率为 ![]() .
.
(Ⅱ)随机变量X的所有可能取值为1,2,3,4. ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以随机变量X的分布列是
X | 1 | 2 | 3 | 4 |
P |
|
|
|
|
随机变量X的数学期望 ![]() .
.
【解析】(Ⅰ)从7个球中取出4个球的所有可能结果数有 ![]() ,然后求出取出的4个球中,含有编号为3的球的结果数,代入古典概率的求解公式即可求解(Ⅱ)先判断随机变量X的所有可能取值为1,2,3,4,根据题意求出随机变量的各个取值的概率,即可求解分布列及期望值
,然后求出取出的4个球中,含有编号为3的球的结果数,代入古典概率的求解公式即可求解(Ⅱ)先判断随机变量X的所有可能取值为1,2,3,4,根据题意求出随机变量的各个取值的概率,即可求解分布列及期望值
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭进行理财投资,根据长期收益率市场预测,投资
 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.(1)分别写出
 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程

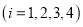 关于时间
关于时间 的函数关系式分别为
的函数关系式分别为 ,
, ,
, ,
,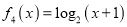 ,有以下结论:
,有以下结论:①当
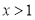 时,甲走在最前面;
时,甲走在最前面;②当
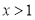 时,乙走在最前面;
时,乙走在最前面;③当
 时,丁走在最前面,当
时,丁走在最前面,当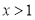 时,丁走在最后面;
时,丁走在最后面;④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E、F分别是BB1 , CD的中点,求证:平面ADE⊥平面A1FD1 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+x2 .
(Ⅰ)求函数h(x)=f(x)﹣3x的极值;
(Ⅱ)若函数g(x)=f(x)﹣ax在定义域内为增函数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,内角A,B,C成等差数列,其对边a,b,c满足2b2=3ac,求A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:函数y=sin2x的最小正周期为
 ;命题q:函数y=cosx的图象关于直线x=
;命题q:函数y=cosx的图象关于直线x=  对称.则下列判断正确的是( )
对称.则下列判断正确的是( )
A.p为真
B.¬q为假
C.p∧q为假
D.p∨q为真
相关试题

