【题目】已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0),f(2)=0,且方程f(x)=x有等根.
(1)求f(x)的解析式
(2)是否存在常数m,n(m<n),使f(x)的定义域和值域分别是[m,n]和[2m,2n]?如存在,求出m,n的值;如不存在,说明理由.
参考答案:
【答案】
(1)解:由题设,方程f (x)=x有等根,即ax2+(b﹣1)x=0有等根,
∴△=0b=1.
又f (2)=0,
∴4a+2b=0,∴a=﹣ ![]() .
.
故f (x)=﹣ ![]() x2+x.
x2+x.
(2)解:∵f (x)=﹣ ![]() x2+x=﹣
x2+x=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ≤
≤ ![]() ,
,
∴2n≤ ![]() ,即 n≤
,即 n≤ ![]() .
.
而当n≤ ![]() 时,f (x)在[m,n]上为增函数,
时,f (x)在[m,n]上为增函数,
设满足条件的m,n存在,则 ![]() 即
即  ,
,
又m<n≤ ![]() ,由上可解得 m=﹣2,n=0.
,由上可解得 m=﹣2,n=0.
即符合条件的m,n存在,其值为m=﹣2,n=0
【解析】(1)利用条件f(2)=0,且方程f(x)=x有等根,建立方程组,求f(x)的解析式(2)利用二次函数的单调性和值域之间的关系建立,方程关系.
【考点精析】认真审题,首先需要了解二次函数的性质(当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减),还要掌握二次函数在闭区间上的最值(当
上递减),还要掌握二次函数在闭区间上的最值(当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
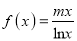 ,曲线
,曲线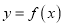 在点
在点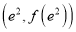 处的切线与直线
处的切线与直线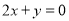 垂直(其中
垂直(其中 为自然对数的底数).
为自然对数的底数).(1)求
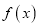 的解析式及单调递减区间;
的解析式及单调递减区间;(2)是否存在常数
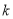 ,使得对于定义域内的任意
,使得对于定义域内的任意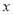 ,
, 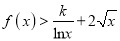 恒成立,若存在,求出
恒成立,若存在,求出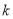 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电x度时,应缴电费y元,写出y关于x的函数关系式;
(2)小明家第一季度缴纳电费情况如表:月份
一月
二月
三月
合计
缴费金额
82元
64元
46.8元
192.8元
问小明家第一季度共用电多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )

A.2
B.1
C.0
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某三棱锥的三视图如图所示,则该三棱锥的表面积是( )

A.2+
B.4+
C.2+2
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 +lg(﹣x2+4x﹣3)的定义域为M,
+lg(﹣x2+4x﹣3)的定义域为M,
(1)求M;
(2)当x∈M时,求函数f(x)=a2x+2+34x(a<﹣3)的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
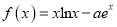 (
(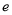 为自然对数的底数)有两个极值点,则实数
为自然对数的底数)有两个极值点,则实数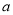 的取值范围是( )
的取值范围是( )A.
 B.
B. 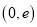 C.
C. 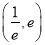 D.
D. 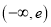
相关试题

