【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时, ![]() ,则对任意
,则对任意![]() ,函数
,函数![]() 的零点个数至多有( )
的零点个数至多有( )
A. 3个 B. 4个 C. 6个 D. 9个
参考答案:
【答案】A
【解析】当![]() 时
时![]() ,由此可知
,由此可知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增, ![]() ,
, ![]() 且
且![]() ,数
,数![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数, ![]() ,而
,而![]() 时,
时, ![]() ,所以
,所以![]() 的图象如图,令
的图象如图,令![]() ,则
,则![]() ,由图可知,当
,由图可知,当![]() 时方程
时方程![]() 至多3个根,当
至多3个根,当![]() 时方程
时方程![]() 没有根,而对任意
没有根,而对任意![]() ,
, ![]() 至多有一个根
至多有一个根![]() ,从而函数
,从而函数![]() 的零点个数至多有3个.
的零点个数至多有3个.
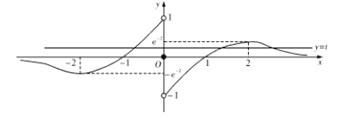
点晴:本题考查函数导数与单调性.确定零点的个数问题:可利用数形结合的办法判断交点个数,如果函数较为复杂,可结合导数知识确定极值点和单调区间从而确定其大致图象.方程的有解问题就是判断是否存在零点的问题,可参变分离,转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组
 ,第二组
,第二组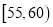 ,…,第五组
,…,第五组 ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为 .
.
(Ⅰ)求
 的值,并求这50名同学心率的平均值;
的值,并求这50名同学心率的平均值;(Ⅱ)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?说明你的理由.
参考数据:

0.15
0.10
0.05
0.025
0.010
0.005
0.001
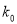
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:
 ,其中
,其中
心率小于60次/分
心率不小于60次/分
合计
体育生
20
艺术生
30
合计
50
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
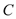 的圆心在直线
的圆心在直线 上,且与直线
上,且与直线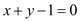 相切于点
相切于点 .
.(1)求圆
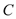 方程;
方程;(2)是否存在过点
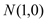 的直线
的直线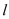 与圆
与圆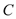 交于
交于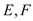 两点,且
两点,且 的面积是
的面积是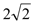 (
(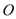 为坐标原点),若存在,求出直线
为坐标原点),若存在,求出直线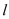 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为
 +
+ =1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________.
=1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过原点的动直线
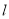 与圆
与圆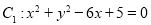 相交于不同的两点
相交于不同的两点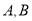 .
.(1)求线段
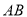 的中点
的中点 的轨迹
的轨迹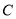 的方程;
的方程;(2)是否存在实数
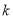 ,使得直线
,使得直线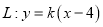 与曲线
与曲线 只有一个交点?若存在,求出
只有一个交点?若存在,求出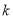 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
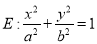 (
(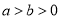 )的离心率为
)的离心率为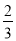 ,
,  分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线 ,使
,使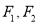 关于
关于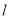 的对称点恰好是圆
的对称点恰好是圆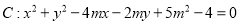 (
(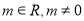 )的一条直线的两个端点.
)的一条直线的两个端点.(1)求椭圆
 的方程;
的方程;(2)设直线
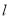 与抛物线
与抛物线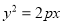 (
(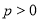 )相交于
)相交于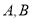 两点,射线
两点,射线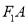 ,
, 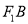 与椭圆
与椭圆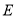 分别相交于点
分别相交于点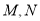 ,试探究:是否存在数集
,试探究:是否存在数集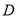 ,当且仅当
,当且仅当 时,总存在
时,总存在 ,使点
,使点 在以线段
在以线段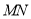 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集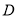 ;若不存在,请说明理由.
;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a,b,c分别为角A,B,C的对边.若acosB=3,bcosA=l,且A﹣B=

(1)求边c的长;
(2)求角B的大小.
相关试题

