【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,
, ![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() (
(![]() )的一条直线的两个端点.
)的一条直线的两个端点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() (
(![]() )相交于
)相交于![]() 两点,射线
两点,射线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别相交于点
分别相交于点![]() ,试探究:是否存在数集
,试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由圆![]() 的方程配方得半径为2,由题设知,椭圆的焦距
的方程配方得半径为2,由题设知,椭圆的焦距![]() 等于圆
等于圆![]() 的直径,所以
的直径,所以![]() ,又
,又![]() ,可得椭圆方程.
,可得椭圆方程.
(2)由题可得直线![]() 是线段
是线段![]() 的垂直平分线,由
的垂直平分线,由![]() 方程与
方程与![]() ,联立可得:
,联立可得:
![]() ,
, ![]() .又点
.又点![]() 在以线段
在以线段![]() 为直径的圆内即
为直径的圆内即![]() ,
, ![]()
试题解析:(1)将圆![]() 的方程配方得:
的方程配方得: ![]() ,所以其圆心为
,所以其圆心为![]() ,半径为2,由题设知,椭圆的焦距
,半径为2,由题设知,椭圆的焦距![]() 等于圆
等于圆![]() 的直径,所以
的直径,所以![]() ,
,
又![]() ,所以
,所以![]() ,从而
,从而![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(2)因为![]() 产于
产于![]() 的对称点恰好是圆
的对称点恰好是圆![]() 的一条直径的两个端点,所以直线
的一条直径的两个端点,所以直线![]() 是线段
是线段![]() 的垂直平分线(
的垂直平分线(![]() 是坐标原点),故
是坐标原点),故![]() 方程为
方程为![]() ,与
,与![]() ,联立得:
,联立得: ![]() ,由其判别式
,由其判别式![]() 得
得![]() ①.
①.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
从而![]() ,
, 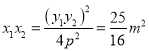 .
.
因为![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,
, ![]() ,
,
注意到![]() 与
与![]() 同向,
同向, ![]() 与
与![]() 同向,所以
同向,所以
点![]() 在以线段
在以线段![]() 为直径的圆内
为直径的圆内![]() ,所以
,所以
![]() 即
即![]()
代入整理得![]() ②
②
当且仅当![]() 即
即![]() 时,总存在
时,总存在![]() ,使②成立.
,使②成立.
又当![]() 时,由韦达定理知方程
时,由韦达定理知方程![]() 的两根均为正数,故使②成立的
的两根均为正数,故使②成立的![]() ,从而满足①.
,从而满足①.
故存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() 使点
使点![]() 在以线段
在以线段![]() 为直径的圆内.
为直径的圆内.
点晴:本题主要考查直线与圆锥曲线位置关系. 直线和圆锥曲线的位置关系一方面要体现方程思想,另一方面要结合已知条件,从图形角度求解.联立直线与圆锥曲线的方程得到方程组,化为一元二次方程后由根与系数的关系求解是一个常用的方法. 涉及点![]() 在以线段
在以线段![]() 为直径的圆内
为直径的圆内![]() ,坐标化求解即可.
,坐标化求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的方程为
 +
+ =1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________.
=1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时,  ,则对任意
,则对任意 ,函数
,函数 的零点个数至多有( )
的零点个数至多有( )A. 3个 B. 4个 C. 6个 D. 9个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过原点的动直线
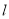 与圆
与圆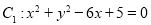 相交于不同的两点
相交于不同的两点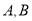 .
.(1)求线段
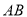 的中点
的中点 的轨迹
的轨迹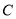 的方程;
的方程;(2)是否存在实数
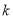 ,使得直线
,使得直线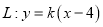 与曲线
与曲线 只有一个交点?若存在,求出
只有一个交点?若存在,求出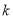 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,a,b,c分别为角A,B,C的对边.若acosB=3,bcosA=l,且A﹣B=

(1)求边c的长;
(2)求角B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】若圆
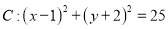 上有四个不同的点到直线
上有四个不同的点到直线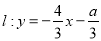 的距离为2,则
的距离为2,则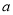 的取值范围是( )
的取值范围是( )A. (-12,8) B. (-8,12) C. (-13,17) D. (-17,13)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
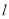 :
: 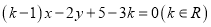 恒过定点
恒过定点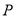 ,圆
,圆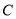 经过点
经过点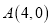 和点
和点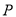 ,且圆心在直线
,且圆心在直线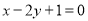 上.
上.(1)求定点
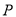 的坐标;
的坐标;(2)求圆
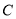 的方程;
的方程;(3)已知点
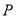 为圆
为圆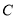 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点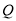 ,问:在
,问:在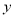 轴上是否存在一点
轴上是否存在一点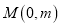 ,使得
,使得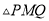 为直角三角形,若存在,求出
为直角三角形,若存在,求出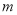 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
相关试题

