【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若![]()
![]() =﹣2,求实数k的值;
=﹣2,求实数k的值;
(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
参考答案:
【答案】(1)x2+y2=4(2)0(3)存在圆P:5x2+5y2﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0)
【解析】
试题分析:(1)设圆心C(a,a),半径为r.|AC|=|BC|=r,由此能求出圆C的方程;(2)由
![]() ,得∠POQ=120°,圆心C到直线l:kx-y+1=0的距离d=1,由此能求出k=0;(3)当直线m的斜率不存在时,圆C也是满足题意的圆;当直线m的斜率存在时,设直线m:y=kx+4,由
,得∠POQ=120°,圆心C到直线l:kx-y+1=0的距离d=1,由此能求出k=0;(3)当直线m的斜率不存在时,圆C也是满足题意的圆;当直线m的斜率存在时,设直线m:y=kx+4,由 ,得(1+k2)x2+8kx+12=0,由此利用根的判别式、韦达定理,结合已知条件能求出在以EF为直径的所有圆中,存在圆P:5x2+5y2﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0).
,得(1+k2)x2+8kx+12=0,由此利用根的判别式、韦达定理,结合已知条件能求出在以EF为直径的所有圆中,存在圆P:5x2+5y2﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0).
试题解析:(1)设圆心C(a,a),半径为r.
因为圆C经过点A(﹣2,0),B(0,2),所以|AC|=|BC|=r,即 ,
,
解得a=0,r=2, 所以圆C的方程是x2+y2=4.…………………3分
(2)因为![]()
![]() =2×2×cos<
=2×2×cos<![]() ,
,![]() >=﹣2,且
>=﹣2,且![]() 与
与![]() 的夹角为∠POQ,
的夹角为∠POQ,
所以cos∠POQ=﹣![]() ,∠POQ=120°,
,∠POQ=120°,
所以圆心C到直线l:kx﹣y+1=0的距离d=1,
又d=![]() ,所以k=0.…………………6分
,所以k=0.…………………6分
(3)(ⅰ)当直线m的斜率不存在时,
直线m经过圆C的圆心C,
此时直线m与圆C的交点为E(0,2),F(0,﹣2),
EF即为圆C的直径,而点M(2,0)在圆C上,
即圆C也是满足题意的圆.…………………7分
(ⅱ)当直线m的斜率存在时,设直线m:y=kx+4,
由![]() ,消去y整理,得(1+k2)x2+8kx+12=0,
,消去y整理,得(1+k2)x2+8kx+12=0,
由△=64k2﹣48(1+k2)>0,得![]() 或
或![]() .
.
设E(x1,y1),F(x2,y2),
则有 ①…………………8分
①…………………8分
由①得![]() ,②
,②![]() ,③…………………9分
,③…………………9分
若存在以EF为直径的圆P经过点M(2,0),则ME⊥MF,
所以![]() ,
,
因此(x1﹣2)(x2﹣2)+y1y2=0,
即x1x2﹣2(x1+x2)+4+y1y2=0,…
则![]() ,
,
所以16k+32=0,k=﹣2,满足题意.…………………10分
此时以EF为直径的圆的方程为x2+y2﹣(x1+x2)x﹣(y1+y2)y+x1x2+y1y2=0,
即![]() ,
,
亦即5x2+5y2﹣16x﹣8y+12=0.…………………11分
综上,在以EF为直径的所有圆中,
存在圆P:5x2+5y2﹣16x﹣8y+12=0或x2+y2=4,使得圆P经过点M(2,0).………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
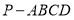 ,底面
,底面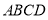 是
是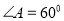 、边长为
、边长为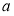 的菱形,又
的菱形,又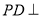 底
底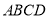 ,且
,且 ,点
,点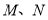 分别是棱
分别是棱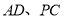 的中点.
的中点.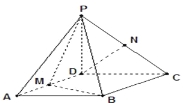
(1)证明:
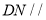 平面
平面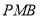 ;
;(2)证明:平面
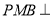 平面
平面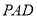 ;
;(3)求点
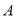 到平面
到平面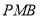 的距离.[
的距离.[ -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆 ,圆
,圆 .
.(1)若过点
 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;(2)圆
 是以1为半径,圆心在圆
是以1为半径,圆心在圆 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆 上任意一点
上任意一点 分别作圆
分别作圆 的两条切线
的两条切线 ,切点为
,切点为 ,求
,求 的取值范围;
的取值范围;(3)若动圆
 同时平分圆
同时平分圆 的周长、圆
的周长、圆 的周长,则动圆
的周长,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
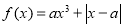 ,
,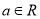 .
.(1)若
 ,求函数
,求函数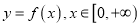 的图象在
的图象在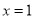 处的切线方程;
处的切线方程;(2)若
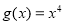 ,试讨论方程
,试讨论方程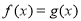 的实数解的个数;
的实数解的个数;(3)当
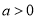 时,若对于任意的
时,若对于任意的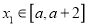 ,都存在
,都存在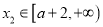 ,使得
,使得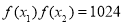 ,求满足条件的正整数
,求满足条件的正整数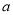 的取值的集合.
的取值的集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的
 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是 ,点
,点 在直径
在直径 上,且
上,且 .
.
(1)若
 米,求
米,求 的长;
的长;(2)设
 , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
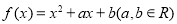 的一个零点为-2,当
的一个零点为-2,当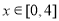 时最大值为0.
时最大值为0.(1)求
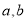 的值;
的值;(2)若对
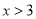 ,不等式
,不等式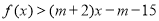 恒成立,求实数
恒成立,求实数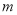 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}的公比q>1,且满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log
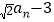 ,Sn=b1+b2+…+bn,求使
,Sn=b1+b2+…+bn,求使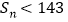 成立的正整数n的最大值.
成立的正整数n的最大值.
相关试题

