【题目】已知四棱锥![]() ,底面
,底面![]() 是
是![]() 、边长为
、边长为![]() 的菱形,又
的菱形,又![]() 底
底![]() ,且
,且![]() ,点
,点![]() 分别是棱
分别是棱![]() 的中点.
的中点.
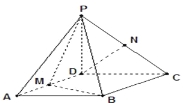
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.[
的距离.[
参考答案:
【答案】(1)详见解析(2)详见解析(3)![]()
【解析】
试题分析:(1)要证DN∥平面PMB,只要证DN∥MQ;(2)要证平面PMB⊥平面PAD,只要证MB⊥平面PAD;
(3)利用PD是三棱锥P-AMB的高PD=2,棱锥A-PMB的体积=棱锥P-AMB的体积,利用棱锥的体积公式解之
试题解析:(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,因为
,因为![]() 分别是棱
分别是棱![]() 中点,
中点,
所以![]() ,且
,且![]() ,于是
,于是![]() ,
,
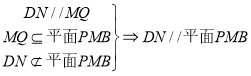 .
.
(2)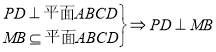 ,
,
又因为底面![]() 是
是![]() 、边长为
、边长为![]() 的菱形,且
的菱形,且![]() 为
为![]() 中点,所以
中点,所以![]() ,又
,又![]() ,
,
所以![]() .
.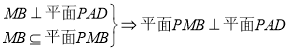 .
.
(3)因为![]() 是
是![]() 中点,所以点
中点,所以点![]() 与
与![]() 到平面
到平面![]() 等距离.过点
等距离.过点![]() 作
作![]() 于
于![]() ,由(2)由平面
,由(2)由平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
故![]() 是点
是点![]() 到平面
到平面![]() 的距离
的距离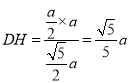 .
.
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中, 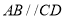 ,
, 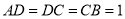 ,
, 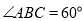 ,四边形
,四边形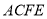 为矩形,平面
为矩形,平面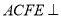 平面
平面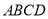 ,
, 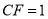 .
.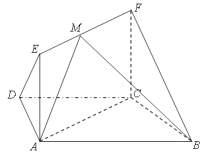
(1)求证:
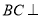 平面
平面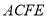 ;
;(2)点
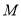 在线段
在线段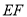 上运动,设平面
上运动,设平面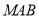 与平面
与平面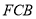 所成二面角的平面角为
所成二面角的平面角为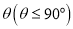 ,试求
,试求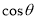 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
 是首项为0的递增数列,
是首项为0的递增数列,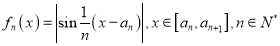 ,满足:对于任意的
,满足:对于任意的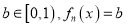 总有两个不同的根,则
总有两个不同的根,则 的通项公式为_________
的通项公式为_________ -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市
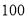 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以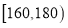 ,
,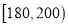 ,
,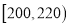 ,
,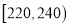 ,
, ,
,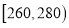 ,
,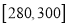 分组的频率分布直方图如图.
分组的频率分布直方图如图.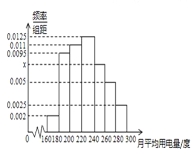
(I)求直方图中
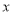 的值;
的值; (II)求月平均用电量的众数和中位数;
(III)在月平均用电量为
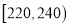 ,
, ,
,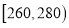 ,
,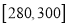 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在
户居民,则月平均用电量在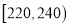 的用户中应抽取多少户?
的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆 ,圆
,圆 .
.(1)若过点
 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;(2)圆
 是以1为半径,圆心在圆
是以1为半径,圆心在圆 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆 上任意一点
上任意一点 分别作圆
分别作圆 的两条切线
的两条切线 ,切点为
,切点为 ,求
,求 的取值范围;
的取值范围;(3)若动圆
 同时平分圆
同时平分圆 的周长、圆
的周长、圆 的周长,则动圆
的周长,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
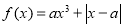 ,
,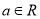 .
.(1)若
 ,求函数
,求函数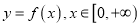 的图象在
的图象在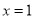 处的切线方程;
处的切线方程;(2)若
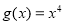 ,试讨论方程
,试讨论方程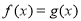 的实数解的个数;
的实数解的个数;(3)当
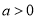 时,若对于任意的
时,若对于任意的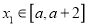 ,都存在
,都存在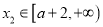 ,使得
,使得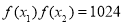 ,求满足条件的正整数
,求满足条件的正整数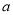 的取值的集合.
的取值的集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若
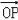
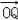 =﹣2,求实数k的值;
=﹣2,求实数k的值;(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
相关试题

