【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若![]() ,试讨论方程
,试讨论方程![]() 的实数解的个数;
的实数解的个数;
(3)当![]() 时,若对于任意的
时,若对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求满足条件的正整数
,求满足条件的正整数![]() 的取值的集合.
的取值的集合.
参考答案:
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
试题分析:(1)去绝对值号后求导,利用导数的几何意义即可求解;(2)对![]() 的取值进行分类讨论,去绝对值号后即可求解;(3)分析题意可知问题等价于函数
的取值进行分类讨论,去绝对值号后即可求解;(3)分析题意可知问题等价于函数![]() 的值域是
的值域是![]() 的子集,从而即可建立关于
的子集,从而即可建立关于![]() 的不等式,即可求解.
的不等式,即可求解.
试题解析:(1)当![]() ,
,![]() 时,
时,![]() ,从而
,从而![]() ,而
,而![]() ,
,![]() ,∴函数
,∴函数![]() ,
,![]() 的图象在
的图象在![]() 处的切线方程为:
处的切线方程为:![]() ,即
,即![]() ;(2)
;(2)![]() 即为
即为![]() ,∴
,∴![]() ,从而
,从而![]() ,此方程等价于
,此方程等价于![]() 或
或![]() 或
或![]() ,
,
∴当![]() 时,方程
时,方程![]() 有两个不同的解
有两个不同的解![]() ,
,![]() ;
;
当![]() 时,方程
时,方程![]() 有三个不同的解
有三个不同的解![]() ,
,![]() ,
,![]() ;
;
当![]() 时,方程
时,方程![]() )有两个不同的解
)有两个不同的解![]() ,
,![]() ;
;
(3)当![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,
∴函数![]() 在
在![]() 是增函数,且
是增函数,且![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
∵对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,
,
∴![]() ,从而
,从而![]() ,
,
∴![]() ,即
,即![]() ,即
,即![]() ,
,
∵![]() ,显然
,显然![]() 满足,而
满足,而![]() 时,均不满足,
时,均不满足,
∴满足条件的正整数![]() 的取值的集合为
的取值的集合为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市
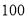 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以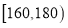 ,
,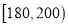 ,
,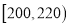 ,
,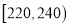 ,
, ,
,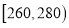 ,
,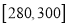 分组的频率分布直方图如图.
分组的频率分布直方图如图.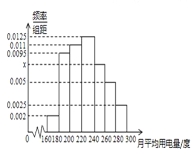
(I)求直方图中
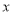 的值;
的值; (II)求月平均用电量的众数和中位数;
(III)在月平均用电量为
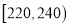 ,
, ,
,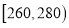 ,
,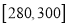 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取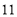 户居民,则月平均用电量在
户居民,则月平均用电量在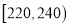 的用户中应抽取多少户?
的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
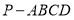 ,底面
,底面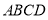 是
是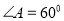 、边长为
、边长为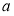 的菱形,又
的菱形,又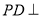 底
底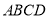 ,且
,且 ,点
,点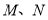 分别是棱
分别是棱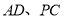 的中点.
的中点.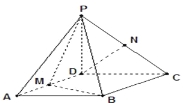
(1)证明:
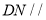 平面
平面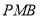 ;
;(2)证明:平面
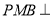 平面
平面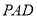 ;
;(3)求点
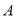 到平面
到平面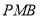 的距离.[
的距离.[ -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆 ,圆
,圆 .
.(1)若过点
 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;(2)圆
 是以1为半径,圆心在圆
是以1为半径,圆心在圆 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆 上任意一点
上任意一点 分别作圆
分别作圆 的两条切线
的两条切线 ,切点为
,切点为 ,求
,求 的取值范围;
的取值范围;(3)若动圆
 同时平分圆
同时平分圆 的周长、圆
的周长、圆 的周长,则动圆
的周长,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若
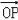
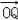 =﹣2,求实数k的值;
=﹣2,求实数k的值;(3)过点(0,4)作动直线m交圆C于E,F两点.试问:在以EF为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的
 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是 ,点
,点 在直径
在直径 上,且
上,且 .
.
(1)若
 米,求
米,求 的长;
的长;(2)设
 , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
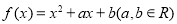 的一个零点为-2,当
的一个零点为-2,当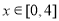 时最大值为0.
时最大值为0.(1)求
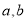 的值;
的值;(2)若对
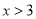 ,不等式
,不等式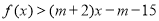 恒成立,求实数
恒成立,求实数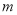 的取值范围.
的取值范围.
相关试题

