【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
参考答案:
【答案】
(1)解:由cos2A﹣3cos(B+C)=1,得2cos2A+3cosA﹣2=0,
即(2cosA﹣1)(cosA+2)=0,解得 ![]() (舍去).
(舍去).
因为0<A<π,所以 ![]() .
.
(2)解:由S= ![]() =
= ![]() =
= ![]() ,得到bc=20.又b=5,解得c=4.
,得到bc=20.又b=5,解得c=4.
由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21,故 ![]() .
.
又由正弦定理得 ![]() .
.
【解析】(1)利用倍角公式和诱导公式即可得出;(2)由三角形的面积公式 ![]() 即可得到bc=20.又b=5,解得c=4.由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21,即可得出a.又由正弦定理得即可得到
即可得到bc=20.又b=5,解得c=4.由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21,即可得出a.又由正弦定理得即可得到 ![]() 即可得出.
即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中, ,其余棱长均为
,其余棱长均为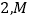 是棱
是棱 上的一点,
上的一点, 分别为棱
分别为棱 的中点.
的中点.
(1)求证: 平面
 平面
平面 ;
;(2)若
 平面
平面 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,…,第n个三角形数为
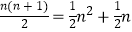 .记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
.记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
三角形数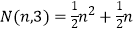 ,
,
正方形数N(n,4)=n2 ,
五边形数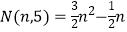 ,
,
六边形数N(n,6)=2n2﹣n,
…
可以推测N(n,k)的表达式,由此计算N(10,24)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4﹣4:坐标系与参数方程)
在直角坐标系xOy中,椭圆C的参数方程为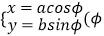 为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为
为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为 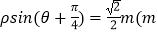 为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 .
为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取10000名进行调查,将受访用户按年龄分成5组:
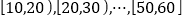 并整理得到如下频率分布直方图:
并整理得到如下频率分布直方图: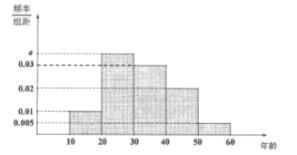
(1)求
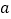 的值;
的值;(2)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于40岁的概率;
(3)估计春节期间参与收发网络红包的手机用户的平均年龄。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 的焦点为
的焦点为 ,点
,点 是抛物线
是抛物线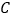 上一点,且
上一点,且 .
.(1)求
 的值;
的值;(2)若
 为抛物线
为抛物线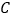 上异于
上异于 的两点,且
的两点,且 .记点
.记点 到直线
到直线 的距离分别为
的距离分别为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
已知函数
 ,其中
,其中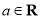 .
.(Ⅰ)当
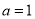 时,求曲线
时,求曲线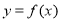 在点
在点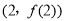 处的切线方程;
处的切线方程;(Ⅱ)当
 时,求函数
时,求函数 的单调区间与极值.
的单调区间与极值.
相关试题

