【题目】如图,在三棱锥![]() 中,
中,![]() ,其余棱长均为
,其余棱长均为![]() 是棱
是棱![]() 上的一点,
上的一点,![]() 分别为棱
分别为棱![]() 的中点.
的中点.

(1)求证: 平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)先证明PE ⊥平面ABC,再证明平面![]() 平面
平面![]() .(2) 连接CD交AE于O,连接OM,先证明PD∥OM,再利用相似求出
.(2) 连接CD交AE于O,连接OM,先证明PD∥OM,再利用相似求出![]() 的长.
的长.
详解:(1)证明:如图,连结PE.

因为△PBC的边长为2的正三角形,E为BC中点,
所以PE⊥BC,
且PE=![]() ,同理AE=
,同理AE=![]() .
.
因为PA=![]() ,所以PE2+AE2=PA2,所以PE⊥AE.
,所以PE2+AE2=PA2,所以PE⊥AE.
因为PE⊥BC,PE⊥AE,BC∩AE=E,AE,BC 平面ABC,
所以PE ⊥平面ABC.
因为PE平面PBC,
所以平面PBC⊥平面ABC.
(2)如图,连接CD交AE于O,连接OM.
因为PD∥平面AEM,PD平面PDC,平面AEM∩平面PDC=OM,
所以PD∥OM, 所以![]() .
.
因为D,E分别为AB,BC的中点,CD∩AE=O,
所以O为ABC重心,所以![]() ,
,
所以PM=![]() PC=
PC=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示:
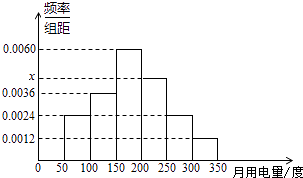
(Ⅰ)直方图中x的值为;
(Ⅱ)在这些用户中,用电量落在区间[100,250)内的户数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
 .
.(1)求不等式
 的解集;
的解集;(2)若
 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读如图所示的程序框图,运行相应的程序,输出的结果i= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,…,第n个三角形数为
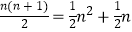 .记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
.记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
三角形数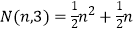 ,
,
正方形数N(n,4)=n2 ,
五边形数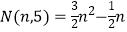 ,
,
六边形数N(n,6)=2n2﹣n,
…
可以推测N(n,k)的表达式,由此计算N(10,24)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4﹣4:坐标系与参数方程)
在直角坐标系xOy中,椭圆C的参数方程为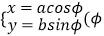 为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为
为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为 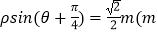 为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 .
为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
相关试题

