【题目】为提高黔东南州的整体旅游服务质量,州旅游局举办了黔东南州旅游知识竞赛,参赛单位为本州内各旅游协会,参赛选手为持证导游.现有来自甲旅游协会的导游3名,其中高级导游2名;乙旅游协会的导游5名,其中高级导游3名.从这8名导游中随机选择4人 参加比赛.
(Ⅰ)设![]() 为事件“选出的4人中恰有2名高级导游,且这2名高级导游来自同一个旅游协会”,求事件
为事件“选出的4人中恰有2名高级导游,且这2名高级导游来自同一个旅游协会”,求事件![]() 发生的概率.
发生的概率.
(Ⅱ)设![]() 为选出的4人中高级导游的人数,求随机变量
为选出的4人中高级导游的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(Ⅰ)由已知条件知,当两名高级导游来自甲旅游协会时,有![]() 种不同选法,当两名高级导游来自乙旅游协会时,有
种不同选法,当两名高级导游来自乙旅游协会时,有![]() 种不同选法,利用古典概型及其概率的计算公式,即可求解事件
种不同选法,利用古典概型及其概率的计算公式,即可求解事件![]() 发生的概率;
发生的概率;
(Ⅱ)由题意,得随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,求得随便取每个值的概率,列出分布列,利用公式求解随机变量的期望.
,求得随便取每个值的概率,列出分布列,利用公式求解随机变量的期望.
试题解析:
(Ⅰ)由已知条件知,当两名高级导游来自甲旅游协会时,有![]() 种不同选法;
种不同选法;
当两名高级导游来自乙旅游协会时,有![]() 种不同选法,则
种不同选法,则
![]() ,所以事件
,所以事件![]() 发生的概率为
发生的概率为![]()
![]() .
.
(Ⅱ)随机变量![]() 的所有可能取值为1,2,3,4.
的所有可能取值为1,2,3,4.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以,随机变量![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 |
|
|
|
|
|
则随机变量![]() 的数学期望
的数学期望![]() (人).
(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生平均每天课外体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)

将学生日均课外体育锻炼时间在
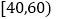 的学生评价为“课外体育达标”.
的学生评价为“课外体育达标”.(1)请根据上述表格中的统计数据填写下面的
 列联表;
列联表;课外体育不达标
课外体育达标
合计
男
女
20
110
合计
(2)通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
参考格式:
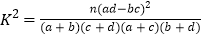 ,其中
,其中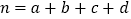
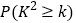
0.025
0.15
0.10
0.005
0.025
0.010
0.005
0.001
5.024
2.072
6.635
7.879
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
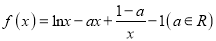
(1)当
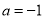 时,求曲线
时,求曲线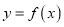 在点
在点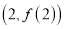 处的切线方程;
处的切线方程;(2)当
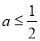 时,讨论
时,讨论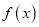 的单调性.
的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】经过中央电视台《魅力中国城》栏目的三轮角逐,黔东南州以三轮竞演总分排名第一名问鼎“最具人气魅力城市”.如图统计了黔东南州从2010年到2017年的旅游总人数(万人次)的变化情况,从一个侧面展示了大美黔东南的魅力所在.根据这个图表,在下列给出的黔东南州从2010年到2017年的旅游总人数的四个判断中,错误的是( )
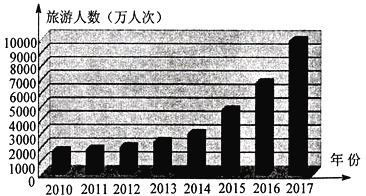
A. 旅游总人数逐年增加
B. 2017年旅游总人数超过2015、2016两年的旅游总人数的和
C. 年份数与旅游总人数成正相关
D. 从2014年起旅游总人数增长加快
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在三棱锥
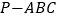 中,
中,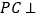 平面
平面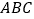 ,
,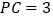 ,
,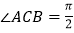 ,
,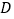 、
、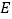 分别为线段
分别为线段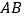 、
、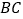 上的点,且
上的点,且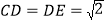 ,
,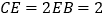 .
.
(Ⅰ)求证:
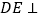 平面
平面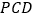 ;
;(Ⅱ)求二面角
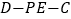 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
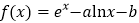 在点
在点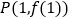 处的切线方程为
处的切线方程为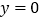 .
.(Ⅰ)求实数
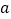 ,
,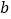 的值;
的值;(Ⅱ)求
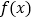 的单调区间;
的单调区间;(Ⅲ)
 ,
,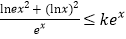 成立,求实数
成立,求实数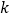 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
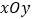 中,点
中,点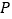 的坐标为
的坐标为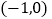 ,直线
,直线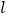 的参数方程为
的参数方程为 (
(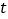 为参数).以坐标原点
为参数).以坐标原点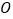 为极点,以
为极点,以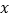 轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆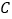 极坐标方程为
极坐标方程为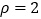 .
.(Ⅰ)当
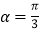 时,求直线
时,求直线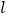 的普通方程和圆
的普通方程和圆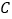 的直角坐标方程;
的直角坐标方程;(Ⅱ)直线
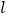 与圆
与圆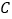 的交点为
的交点为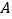 、
、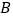 ,证明:
,证明: 是与
是与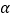 无关的定值.
无关的定值.
相关试题

