【题目】已知函数![]()
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,讨论
时,讨论![]() 的单调性.
的单调性.
参考答案:
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:本题主要考查导数的运算、利用导数求曲线的切线方程、利用导数求函数的单调性等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,先将![]() 代入得到
代入得到![]() 表达式,对
表达式,对![]() 求导,将切点的横坐标2代入
求导,将切点的横坐标2代入![]() 中得到切线的斜率k,再将切点的横坐标2代入到
中得到切线的斜率k,再将切点的横坐标2代入到![]() 中,得到切点的纵坐标,最后利用点斜式写出切线方程;第二问,讨论
中,得到切点的纵坐标,最后利用点斜式写出切线方程;第二问,讨论![]() 的单调性即讨论
的单调性即讨论![]() 的正负,即讨论导数表达式分子的正负,所以构造函数
的正负,即讨论导数表达式分子的正负,所以构造函数![]() ,通过分析题意,将
,通过分析题意,将![]() 分成
分成![]() 、
、![]() 、
、![]() 、
、![]() 多种情况,分类讨论,判断
多种情况,分类讨论,判断![]() 的正负,从而得到
的正负,从而得到![]() 的单调性.
的单调性.
试题解析:(1)当![]() 时,
时, ![]()
![]() 6分
6分
(2)因为![]() ,
,
所以![]()
![]()
![]() ,
,
令![]()
![]() 8分
8分
(i)当a=0时, ![]()
所以当![]() 时g(x)>0,
时g(x)>0, ![]() 此时函数
此时函数![]() 单调递减,
单调递减,
x∈(1,∞)时,g(x)<0, ![]() 此时函数f,(x)单调递增。
此时函数f,(x)单调递增。
(ii)当![]() 时,由
时,由![]() ,解得:
,解得: ![]() 10分
10分
①若![]() ,函数f(x)在
,函数f(x)在![]() 上单调递减, 11分
上单调递减, 11分
②若![]() ,在
,在![]() 单调递减,在
单调递减,在![]() 上单调递增.
上单调递增.
③ 当a<0时,由于1/a-1<0,
x∈(0,1)时,g(x)>0,此时![]() ,函数f(x)单调递减;
,函数f(x)单调递减;
x∈(1,∞)时,g(x)<0 , ![]() ,此时函数
,此时函数![]() 单调递增。
单调递增。
综上所述:
当a≤ 0 时,函数f(x)在(0,1)上单调递减;
函数f(x)在 (1, +∞) 上单调递增
当![]() 时,函数f(x)在(0, + ∞)上单调递减
时,函数f(x)在(0, + ∞)上单调递减
当![]() 时,函数f(x)在
时,函数f(x)在![]() 上单调递减;
上单调递减;
函数 f(x)在![]() 上单调递增; 14分
上单调递增; 14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲设函数
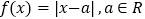
(1)当
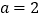 时,解不等式:
时,解不等式: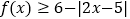 ;
;(2)若关于x的不等式f(x)≤4的解集为[﹣1,7],且两正数s和t满足
 ,求证:
,求证: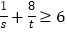 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
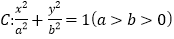 的离心率为
的离心率为 ,且经过点
,且经过点 .
.(1)求椭圆的标准方程;
(2)过点
 的直线
的直线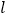 交椭圆于
交椭圆于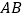 两点,
两点, 是
是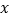 轴上的点,若
轴上的点,若 是以
是以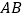 为斜边的等腰直角三角形, 求直线
为斜边的等腰直角三角形, 求直线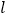 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生平均每天课外体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)

将学生日均课外体育锻炼时间在
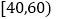 的学生评价为“课外体育达标”.
的学生评价为“课外体育达标”.(1)请根据上述表格中的统计数据填写下面的
 列联表;
列联表;课外体育不达标
课外体育达标
合计
男
女
20
110
合计
(2)通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
参考格式:
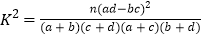 ,其中
,其中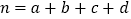
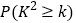
0.025
0.15
0.10
0.005
0.025
0.010
0.005
0.001
5.024
2.072
6.635
7.879
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过中央电视台《魅力中国城》栏目的三轮角逐,黔东南州以三轮竞演总分排名第一名问鼎“最具人气魅力城市”.如图统计了黔东南州从2010年到2017年的旅游总人数(万人次)的变化情况,从一个侧面展示了大美黔东南的魅力所在.根据这个图表,在下列给出的黔东南州从2010年到2017年的旅游总人数的四个判断中,错误的是( )
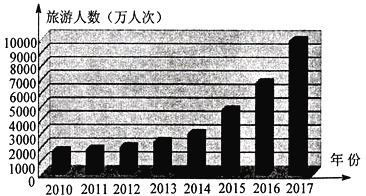
A. 旅游总人数逐年增加
B. 2017年旅游总人数超过2015、2016两年的旅游总人数的和
C. 年份数与旅游总人数成正相关
D. 从2014年起旅游总人数增长加快
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高黔东南州的整体旅游服务质量,州旅游局举办了黔东南州旅游知识竞赛,参赛单位为本州内各旅游协会,参赛选手为持证导游.现有来自甲旅游协会的导游3名,其中高级导游2名;乙旅游协会的导游5名,其中高级导游3名.从这8名导游中随机选择4人 参加比赛.
(Ⅰ)设
 为事件“选出的4人中恰有2名高级导游,且这2名高级导游来自同一个旅游协会”,求事件
为事件“选出的4人中恰有2名高级导游,且这2名高级导游来自同一个旅游协会”,求事件 发生的概率.
发生的概率.(Ⅱ)设
 为选出的4人中高级导游的人数,求随机变量
为选出的4人中高级导游的人数,求随机变量 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在三棱锥
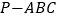 中,
中,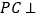 平面
平面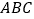 ,
,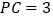 ,
,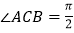 ,
,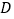 、
、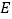 分别为线段
分别为线段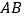 、
、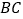 上的点,且
上的点,且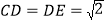 ,
,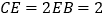 .
.
(Ⅰ)求证:
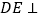 平面
平面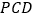 ;
;(Ⅱ)求二面角
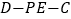 的余弦值.
的余弦值.
相关试题

