【题目】已知函数f(x)=Asin(ωx﹣ ![]() )(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示.
)(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示. 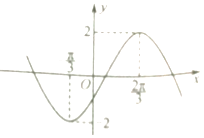
(1)求函数f(x)的解析式;
(2)若f(α+ ![]() )=
)= ![]() ,f(β+
,f(β+ ![]() )=
)= ![]() ,且α,β∈(0,
,且α,β∈(0, ![]() ),求α+β的值.
),求α+β的值.
参考答案:
【答案】
(1)解:据函数y=f(x)的解析式及其图象可知A=2,
且 ![]() T=
T= ![]() ﹣(﹣
﹣(﹣ ![]() )=π,其中T为函数y=f(x)的最小正周期,故T=2π,
)=π,其中T为函数y=f(x)的最小正周期,故T=2π,
所以 ![]() =2π,解得ω=1,
=2π,解得ω=1,
所以f(x)=2sin(x﹣ ![]() ).
).
(2)解:由f(α+ ![]() )=
)= ![]() ,可知2sin(
,可知2sin( ![]() ﹣
﹣ ![]() )=
)= ![]() ,即sinα=
,即sinα= ![]() ,
,
因为α∈(0, ![]() ),
),
所以cos ![]() =
= ![]() =
= ![]() .
.
由f(β+ ![]() )=
)= ![]() ,可知2sin(
,可知2sin( ![]() ﹣
﹣ ![]() )=
)= ![]() ,即sin(x+
,即sin(x+ ![]() )=
)= ![]() ,
,
故cosβ= ![]() ,
,
因为β∈(0, ![]() ),
),
所以sin ![]() =
= ![]() ,
,
于是cos(α+β)=cosαcosβ﹣sinαsinβ= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]() .
.
因为α,β∈(0, ![]() ),
),
所以α+β∈(0,π),
所以α+β= ![]() .
.
【解析】(1)由图可知A的值,由T,可求ω,从而可求函数f(x)的解析式.(2)由f(α+ ![]() )=
)= ![]() ,可知sinα,利用同角三角函数基本关系式可求cosα,由f(β+
,可知sinα,利用同角三角函数基本关系式可求cosα,由f(β+ ![]() )=
)= ![]() ,可知cosβ,利用同角三角函数基本关系式可求sinβ,利用两角和的余弦函数公式可求cos(α+β),结合范围α+β∈(0,π),即可得解α+β的值.
,可知cosβ,利用同角三角函数基本关系式可求sinβ,利用两角和的余弦函数公式可求cos(α+β),结合范围α+β∈(0,π),即可得解α+β的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知E,F分别是棱长为1的正方体ABCD﹣A1B1C1D1的棱BC,CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|f(x)=lg(x﹣1)+
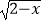 },集合B={y|y=2x+a,x≤0}.
},集合B={y|y=2x+a,x≤0}.
(1)若a= ,求A∪B;
,求A∪B;
(2)若A∩B=,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过抛物线y2=2px(p>0)的焦点,斜率为2
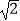 的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若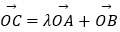 ,求λ的值.
,求λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD

(1)求二面角B﹣AD﹣F的大小;
(2)求直线BD与EF所成的角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线实轴长为6,一条渐近线方程为4x﹣3y=0.过双曲线的右焦点F作倾斜角为
 的直线交双曲线于A、B两点
的直线交双曲线于A、B两点
(1)求双曲线的方程;
(2)求线段AB的中点C到焦点F的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】若|
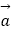 |=1,|
|=1,| 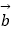 |=m,|
|=m,| 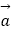 +
+ 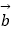 |=2.
|=2.
(1)若|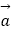 +2
+2 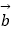 |=3,求实数m的值;
|=3,求实数m的值;
(2)若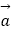 +
+ 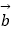 与
与 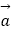 ﹣
﹣ 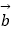 的夹角为
的夹角为 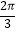 ,求实数m的值.
,求实数m的值.
相关试题

