【题目】已知过抛物线y2=2px(p>0)的焦点,斜率为2 ![]() 的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若 ![]() ,求λ的值.
,求λ的值.
参考答案:
【答案】
(1)解:直线AB的方程是y=2 ![]() (x﹣
(x﹣ ![]() ),与y2=2px联立,有4x2﹣5px+p2=0,
),与y2=2px联立,有4x2﹣5px+p2=0,
∴x1+x2= ![]()
由抛物线定义得:|AB|=x1+x2+p=9
∴p=4,∴抛物线方程是y2=8x
(2)解:由p=4,4x2﹣5px+p2=0得:x2﹣5x+4=0,
∴x1=1,x2=4,
y1=﹣2 ![]() ,y2=4
,y2=4 ![]() ,从而A(1,﹣2
,从而A(1,﹣2 ![]() ),B(4,4
),B(4,4 ![]() ).
).
设 ![]() =(x3,y3)=(1,﹣2
=(x3,y3)=(1,﹣2 ![]() )+λ(4,4
)+λ(4,4 ![]() )=(4λ+1,4
)=(4λ+1,4 ![]() λ﹣2
λ﹣2 ![]() )
)
又[2 ![]() (2λ﹣1)]2=8(4λ+1),解得:λ=0,或λ=2
(2λ﹣1)]2=8(4λ+1),解得:λ=0,或λ=2
【解析】(1)直线AB的方程与y2=2px联立,有4x2﹣5px+p2=0,从而x1+x2= ![]() ,再由抛物线定义得:|AB|=x1+x2+p=9,求得p,则抛物线方程可得.(2)由p=4,4x2﹣5px+p2=0求得A(1,﹣2
,再由抛物线定义得:|AB|=x1+x2+p=9,求得p,则抛物线方程可得.(2)由p=4,4x2﹣5px+p2=0求得A(1,﹣2 ![]() ),B(4,4
),B(4,4 ![]() ).再求得设
).再求得设 ![]() 的坐标,最后代入抛物线方程即可解得λ.
的坐标,最后代入抛物线方程即可解得λ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过点M(﹣2,0)的直线l与椭圆x2+2y2=2交于P1 , P2 , 线段P1P2的中点为P.设直线l的斜率为k1(k1≠0),直线OP的斜率为k2 , 则k1k2等于( )
A.﹣2
B.2
C.
D.﹣
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知E,F分别是棱长为1的正方体ABCD﹣A1B1C1D1的棱BC,CC1的中点,则截面AEFD1与底面ABCD所成二面角的正弦值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|f(x)=lg(x﹣1)+
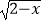 },集合B={y|y=2x+a,x≤0}.
},集合B={y|y=2x+a,x≤0}.
(1)若a= ,求A∪B;
,求A∪B;
(2)若A∩B=,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx﹣
 )(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示.
)(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示. 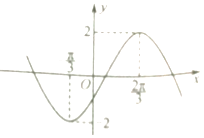
(1)求函数f(x)的解析式;
(2)若f(α+ )=
)= 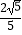 ,f(β+
,f(β+ 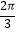 )=
)= 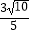 ,且α,β∈(0,
,且α,β∈(0,  ),求α+β的值.
),求α+β的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD

(1)求二面角B﹣AD﹣F的大小;
(2)求直线BD与EF所成的角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线实轴长为6,一条渐近线方程为4x﹣3y=0.过双曲线的右焦点F作倾斜角为
 的直线交双曲线于A、B两点
的直线交双曲线于A、B两点
(1)求双曲线的方程;
(2)求线段AB的中点C到焦点F的距离.
相关试题

