【题目】若| ![]() |=1,|
|=1,| ![]() |=m,|
|=m,| ![]() +
+ ![]() |=2.
|=2.
(1)若| ![]() +2
+2 ![]() |=3,求实数m的值;
|=3,求实数m的值;
(2)若 ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为
的夹角为 ![]() ,求实数m的值.
,求实数m的值.
参考答案:
【答案】
(1)证明:因为| ![]() +
+ ![]() |=2,所以|
|=2,所以| ![]() +
+ ![]() |2=4.
|2=4.
即以 ![]() 2+
2+ ![]() 2+2
2+2 ![]()
![]() =4.,
=4.,
又| ![]() |=1,|
|=1,| ![]() |=m,所以
|=m,所以 ![]() .
.
由| ![]() +2
+2 ![]() |=3,所以所以|
|=3,所以所以| ![]() +2
+2 ![]() |2=9.
|2=9.
即以 ![]() 2+4
2+4 ![]() 2+4
2+4 ![]()
![]() =9,
=9,
所以1+4× ![]() +4m2=9,解得m=±1,
+4m2=9,解得m=±1,
又| ![]() |≥0,所以m=1.
|≥0,所以m=1.
(2)证明:因为,| ![]() |=1,|
|=1,| ![]() |=m,
|=m, ![]()
所以| ![]() ﹣
﹣ ![]() |2=
|2= ![]() 2+
2+ ![]() 2﹣2
2﹣2 ![]()
![]() =1﹣2×
=1﹣2× ![]() +m2=2m2﹣2,|
+m2=2m2﹣2,| ![]() ﹣
﹣ ![]() |=
|= ![]() .
.
又因为 ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为
的夹角为 ![]() ,所以(
,所以( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=以
)=以 ![]() 2﹣
2﹣ ![]() 2=|
2=| ![]() +
+ ![]() |×|
|×| ![]() ﹣
﹣ ![]() |cos
|cos ![]()
即,所以1﹣m2=2× ![]() ,解得m=±
,解得m=± ![]() ,
,
又| ![]() |≥0,所以m=
|≥0,所以m= ![]() .
.
【解析】(1)由| ![]() +
+ ![]() |=2,|
|=2,| ![]() +2
+2 ![]() |=3
|=3 ![]() 2+
2+ ![]() 2+2
2+2 ![]()
![]() =4 和
=4 和 ![]() 2+4
2+4 ![]() 2+4
2+4 ![]()
![]() =9,即可求解;(2)利用(
=9,即可求解;(2)利用( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=以
)=以 ![]() 2﹣
2﹣ ![]() 2=|
2=| ![]() +
+ ![]() |×|
|×| ![]() ﹣
﹣ ![]() |cos
|cos ![]() 求解.
求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx﹣
 )(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示.
)(其中A,ω为常数,且A>0,ω>0)的部分图象如图所示. 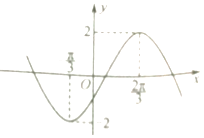
(1)求函数f(x)的解析式;
(2)若f(α+ )=
)= 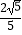 ,f(β+
,f(β+ 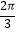 )=
)= 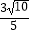 ,且α,β∈(0,
,且α,β∈(0,  ),求α+β的值.
),求α+β的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD

(1)求二面角B﹣AD﹣F的大小;
(2)求直线BD与EF所成的角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线实轴长为6,一条渐近线方程为4x﹣3y=0.过双曲线的右焦点F作倾斜角为
 的直线交双曲线于A、B两点
的直线交双曲线于A、B两点
(1)求双曲线的方程;
(2)求线段AB的中点C到焦点F的距离. -
科目: 来源: 题型:
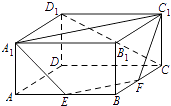
查看答案和解析>>【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点.证明A1 , C1 , F,E四点共面,并求直线CD1与平面A1C1FE所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过村庄A有两条互相垂直的笔直公路AB和AC,根据规划拟在两条公路围成的直角区域内建一工厂P,为了仓库存储和运输方便,在两条公路上分别建两个仓库M,N(异于村庄A,将工厂P及仓库M,N近似看成点,且M,N分别在射线AB,AC上),要求MN=2,PN=1(单位:km),PN⊥MN.
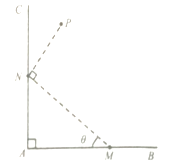
(1)设∠AMN=θ,将工厂与村庄的距离PA表示为θ的函数,记为l(θ),并写出函数l(θ)的定义域;
(2)当θ为何值时,l(θ)有最大值?并求出该最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=m(sinx+cosx)﹣4sinxcosx,x∈[0,
 ],m∈R.
],m∈R.
(1)设t=sinx+cosx,x∈[0, ],将f(x)表示为关于t的函数关系式g(t),并求出t的取值范围;
],将f(x)表示为关于t的函数关系式g(t),并求出t的取值范围;
(2)若关于x的不等式f(x)≥0对所有的x∈[0, ]恒成立,求实数m的取值范围;
]恒成立,求实数m的取值范围;
(3)若关于x的方程f(x)﹣2m+4=0在[0, ]上有实数根,求实数m的取值范围.
]上有实数根,求实数m的取值范围.
相关试题

