【题目】(本小题满分为16分)为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,新上了把二氧化碳处理转化为一种可利用的化工产品的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为:
 ,且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
,且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
参考答案:
【答案】(1)不会获利,至少补贴5 000元(2)400
【解析】
试题分析:(1)解决实际问题关键为读懂题意:能否获利,决定于利润是否为正,故列出利润S函数关系式S=200x-![]() =-
=-![]() x2+400x-80 000=-
x2+400x-80 000=-![]() (x-400)2,当x∈[200,300]时,S<0,因此该单位不会获利,补贴的标准为S取得最大值-5 000,而不是最小值(2)先列出每吨的平均处理成本的函数关系式,为一个分段函数,需分段求最值,最后比较两段最小值的较小值为所求.
(x-400)2,当x∈[200,300]时,S<0,因此该单位不会获利,补贴的标准为S取得最大值-5 000,而不是最小值(2)先列出每吨的平均处理成本的函数关系式,为一个分段函数,需分段求最值,最后比较两段最小值的较小值为所求.
试题解析:(1)当x∈[200,300]时,设该项目获利为S,
则S=200x-![]() =-
=-![]() x2+400x-80 000=-
x2+400x-80 000=-![]() (x-400)2,
(x-400)2,
所以当x∈[200,300]时,S<0,因此该单位不会获利.
当x=300时,S取得最大值-5 000,
所以国家每月至少补贴5 000元才能使该项目不亏损.
(2)由题意可知二氧化碳的每吨处理成本为
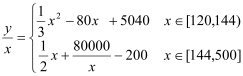
①当x∈[120,144)时,![]() =
=![]() x2-80x+5 040=
x2-80x+5 040=![]() (x-120)2+240,
(x-120)2+240,
所以当x=120时,![]() 取得最小值240.
取得最小值240.
②当x∈[144,500]时,![]() =
=![]() x+
x+![]() -200≥2
-200≥2![]() -200=200,
-200=200,
当且仅当![]() x=
x=![]() ,即x=400时,
,即x=400时,![]() 取得最小值200.因为200<240,
取得最小值200.因为200<240,
答:当每月的处理量为400吨时,才能使每吨的平均处理成本最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.

(1)求证:BD1∥平面A1DE;
(2)求直线A1E与平面AD1E所成角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三内角A,B,C所对的边分别是a,b,c,△ABC的面积S=
 且sinA=
且sinA= 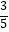 .
.
(1)求sinB;
(2)若边c=5,求△ABC的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的两个焦点坐标分别是F1(﹣
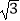 ,0)、F2(
,0)、F2( 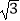 ,0),并且经过点P(
,0),并且经过点P( 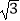 ,﹣
,﹣  ).
).
(1)求椭圆C的方程;
(2)若直线l与圆O:x2+y2=1相切,并与椭圆C交于不同的两点A、B.当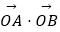 =λ,且满足
=λ,且满足  ≤λ≤
≤λ≤  时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司过去五个月的广告费支出x与销售额y(单位:万元)之间有下列对应数据:
x
2
4
5
6
8
y

40
60
50
70
工作人员不慎将表格中y的第一个数据丢失.已知y对x呈线性相关关系,且回归方程为
 =6.5x+17.5,则下列说法:
=6.5x+17.5,则下列说法:
①销售额y与广告费支出x正相关;
②丢失的数据(表中 处)为30;
处)为30;
③该公司广告费支出每增加1万元,销售额一定增加6.5万元;
④若该公司下月广告投入8万元,则销售额为70万元.
其中,正确说法有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如表:
x
﹣


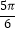
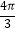
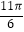
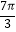
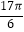
y
﹣1
1
3
1
﹣1
1
3
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果:
( i)当x∈[0, ]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
]时,方程f(3x)=m恰有两个不同的解,求实数m的取值范围;
( ii)若α,β是锐角三角形的两个内角,试比较f(sinα)与f(cosβ)的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列an}的前n项和为Sn , a1=1,a2=2,且点(Sn , Sn+1)在直线y=tx+1上.
(1)求Sn及an;
(2)若数列{bn}满足bn=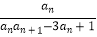 (n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
(n≥2),b1=1,数列{bn}的前n项和为Tn , 求证:当n≥2时,Tn<2.
相关试题

