【题目】已知以点 ![]() 为圆心的圆与直线
为圆心的圆与直线 ![]() 相切,过点
相切,过点 ![]() 的直线
的直线 ![]() 与圆
与圆 ![]() 相交于
相交于 ![]() 两点,
两点, ![]() 是
是 ![]() 的中点,
的中点, ![]() .
.
(1)求圆 ![]() 的标准方程;
的标准方程;
(2)求直线 ![]() 的方程.
的方程.
参考答案:
【答案】
(1)解:设圆 ![]() 的半径为
的半径为 ![]() ,因为圆
,因为圆 ![]() 与直线
与直线 ![]() 相切,
相切,
∴ ![]() ,∴圆
,∴圆 ![]() 的方程为
的方程为 ![]()
(2)解:①当直线 ![]() 与
与 ![]() 轴垂直时,易知
轴垂直时,易知 ![]() 符合题意;
符合题意;
②当直线 ![]() 与
与 ![]() 轴不垂直时,设直线的方程为
轴不垂直时,设直线的方程为 ![]() ,即
,即 ![]() ,
,
连接 ![]() ,则
,则 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
,
则由 ![]() 得
得 ![]() ,∴直线
,∴直线 ![]() 为:
为: ![]() ,
,
故直线 ![]() 的方程为
的方程为 ![]() 或
或 ![]() .
.
【解析】(1)利用点到直线的距离公式求出圆A的半径即可。
(2)分别就直线l是否与x轴垂直展开讨论。垂直时,易知 x = 2 符合题意;不垂直时,根据设出的l的方程表示出AQ后可以求出l的斜率,进而求出l的方程。
【考点精析】关于本题考查的一般式方程和点到直线的距离公式,需要了解直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0);点
(A,B不同时为0);点![]() 到直线
到直线![]() 的距离为:
的距离为: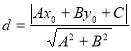 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1:y=cos x,C2:y=sin (2x+
 ),则下面结论正确的是( )
),则下面结论正确的是( )A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
 个单位长度,得到曲线C2
个单位长度,得到曲线C2B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
 个单位长度,得到曲线C2
个单位长度,得到曲线C2C. 把C1上各点的横坐标缩短到原来的
 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2D. 把C1上各点的横坐标缩短到原来的
 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品在30天内每克的销售价格
 (元)与时间
(元)与时间 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段 ,
, (不包含
(不包含 ,
, 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量 (克)与时间
(克)与时间 (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.第
 天
天5
1
5
2
0
3
0
销售量
 克
克3
5
2
5
2
0
1
0

(1)根据提供的图象,写出该商品每克销售的价格
 (元)与时间
(元)与时间 的函数关系式;
的函数关系式;(2)根据表中数据写出一个反映日销售量
 随时间
随时间 变化的函数关系式;
变化的函数关系式;(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的
 值.
值.(注:日销售金额=每克的销售价格×日销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点为
的右焦点为  ,上顶点为
,上顶点为  ,
,  周长为
周长为  ,离心率为
,离心率为  .
.
(1)求椭圆 的方程;
的方程;
(2)若点 是椭圆
是椭圆  上第一象限内的一个点,直线
上第一象限内的一个点,直线  过点
过点  且与直线
且与直线  平行,直线
平行,直线  且
且  与椭圆
与椭圆  交于
交于  两点,与
两点,与  交于点
交于点  ,是否存在常数
,是否存在常数  ,使
,使  .若存在,求出
.若存在,求出  的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点
 为圆心的圆过点
为圆心的圆过点 和
和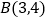 ,线段
,线段 的垂直平分线交圆
的垂直平分线交圆 于点
于点 、
、 ,且
,且 ,
,(1)求直线
 的方程; (2)求圆
的方程; (2)求圆 的方程。
的方程。(3)设点
 在圆
在圆 上,试探究使
上,试探究使 的面积为 8 的点
的面积为 8 的点 共有几个?证明你的结论
共有几个?证明你的结论 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 经过
经过 两点,且圆心在直线
两点,且圆心在直线 上.
上.(Ⅰ)求圆
 的标准方程;
的标准方程;(Ⅱ)设直线
 经过点
经过点 ,且
,且 与圆
与圆 相交所得弦长为
相交所得弦长为 ,求直线
,求直线 的方程.
的方程.
相关试题

