【题目】已知椭圆 ![]() 的右焦点为
的右焦点为 ![]() ,上顶点为
,上顶点为 ![]() ,
, ![]() 周长为
周长为 ![]() ,离心率为
,离心率为 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)若点 ![]() 是椭圆
是椭圆 ![]() 上第一象限内的一个点,直线
上第一象限内的一个点,直线 ![]() 过点
过点 ![]() 且与直线
且与直线 ![]() 平行,直线
平行,直线 ![]() 且
且 ![]() 与椭圆
与椭圆 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 交于点
交于点 ![]() ,是否存在常数
,是否存在常数 ![]() ,使
,使 ![]() .若存在,求出
.若存在,求出 ![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
参考答案:
【答案】
(1)解:由题意知 ![]() ,
, ![]() ,
,
又 ![]() ,∴
,∴ ![]() ,
, ![]() ,
,
∴椭圆 ![]() 的方程为
的方程为 ![]() .
.
(2)解:由 ![]() 得
得 ![]() ,∴
,∴ ![]() ,
,
又 ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() 的方程为
的方程为 ![]() ,可设
,可设 ![]() 方程为
方程为 ![]() ,
,
由 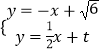 得
得 ![]() ,
,
由 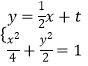 得
得 ![]() ,
, ![]() ,
, ![]() ,
,
设 ![]() ,
, ![]() ,则
,则 ![]() ,
, ![]() ,
,
由弦长公式: ![]() ,
,
同理, ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴存在常数 ![]() ,使
,使 ![]()
【解析】(1)考查了椭圆的几何性质与标准方程。
(2)考查了椭圆的综合应用、弦长公式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品在30天内每克的销售价格
 (元)与时间
(元)与时间 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段 ,
, (不包含
(不包含 ,
, 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量 (克)与时间
(克)与时间 (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.第
 天
天5
1
5
2
0
3
0
销售量
 克
克3
5
2
5
2
0
1
0

(1)根据提供的图象,写出该商品每克销售的价格
 (元)与时间
(元)与时间 的函数关系式;
的函数关系式;(2)根据表中数据写出一个反映日销售量
 随时间
随时间 变化的函数关系式;
变化的函数关系式;(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的
 值.
值.(注:日销售金额=每克的销售价格×日销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点
 为圆心的圆与直线
为圆心的圆与直线  相切,过点
相切,过点  的直线
的直线 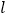 与圆
与圆  相交于
相交于  两点,
两点,  是
是  的中点,
的中点,  .
.
(1)求圆 的标准方程;
的标准方程;
(2)求直线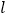 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知以点
 为圆心的圆过点
为圆心的圆过点 和
和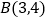 ,线段
,线段 的垂直平分线交圆
的垂直平分线交圆 于点
于点 、
、 ,且
,且 ,
,(1)求直线
 的方程; (2)求圆
的方程; (2)求圆 的方程。
的方程。(3)设点
 在圆
在圆 上,试探究使
上,试探究使 的面积为 8 的点
的面积为 8 的点 共有几个?证明你的结论
共有几个?证明你的结论 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 经过
经过 两点,且圆心在直线
两点,且圆心在直线 上.
上.(Ⅰ)求圆
 的标准方程;
的标准方程;(Ⅱ)设直线
 经过点
经过点 ,且
,且 与圆
与圆 相交所得弦长为
相交所得弦长为 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:
 )分别为
)分别为  ,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A. 的平均数
的平均数
B. 的标准差
的标准差
C. 的最大值
的最大值
D. 的中位数
的中位数
相关试题

