【题目】已知点![]() 是椭圆
是椭圆![]() 的左、右顶点,
的左、右顶点, ![]() 为左焦点,点
为左焦点,点![]() 是椭圆上异于
是椭圆上异于![]() 的任意一点,直线
的任意一点,直线![]() 与过点
与过点![]() 且垂直于
且垂直于![]() 轴的直线
轴的直线![]() 交于点
交于点![]() ,直线
,直线![]() 于点
于点![]() .
.
(1)求证:直线![]() 与直线
与直线![]() 的斜率之积为定值;
的斜率之积为定值;
(2)若直线![]() 过焦点
过焦点![]() ,
, ![]() ,求实数
,求实数![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)设![]() ,利用点在椭圆上的条件,化简
,利用点在椭圆上的条件,化简![]() ,得到定值;(2)设直线
,得到定值;(2)设直线![]() 的斜率分别是
的斜率分别是![]() ,并且表示直线
,并且表示直线![]() ,以及求出交点
,以及求出交点![]() 的坐标,根据
的坐标,根据![]() ,表示直线
,表示直线![]() 的斜率,根据
的斜率,根据![]() 三点共线,表示
三点共线,表示![]() ,得到
,得到![]() 的齐次方程,求
的齐次方程,求![]() 的值,并且代入求
的值,并且代入求![]() 的值.
的值.
试题解析:(1)证明:设![]() ,由已知
,由已知![]() ,
,
∴![]() .①
.①
∵点![]() 在椭圆上,∴
在椭圆上,∴![]() .②
.②
由①②得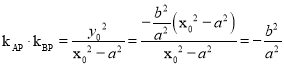 (定值).
(定值).
∴直线![]() 与直线
与直线![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
(2)设直线![]() 与
与![]() 斜率分别为
斜率分别为![]() ,由已知
,由已知![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
直线![]() ,则
,则![]() .
.
∵![]() ,∴
,∴![]() .
.
由(1)知![]() ,故
,故![]() ,
,
又![]() 三点共线,得
三点共线,得![]() ,
,
即![]() ,得
,得![]() .
.
∵![]() ,∴
,∴![]() ,
,
![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
由已知![]() ,得
,得![]() ,
,
将![]() 代入,得
代入,得![]() ,故
,故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
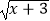 +
+ 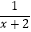 的定义域为( )
的定义域为( )
A.{x|x≥﹣3且x≠﹣2}
B.{x|x≥﹣3且x≠2}
C.{x|x≥﹣3}
D.{x|x≥﹣2且x≠3} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数F(x)=g(x)+h(x)=ex , 且g(x),h(x)分别是R上的偶函数和奇函数,若对任意的x∈(0,+∞),不等式g(2x)≥ah(x)恒成立,则实数a的取值范围是( )
A.(﹣∞,2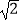 ]
]
B.(﹣∞,2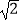 )
)
C.(﹣∞,2]
D.(﹣∞,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N* , 有2Sn=2pan2+pan﹣p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记bn= ,求数列{bn}的前n项和T.
,求数列{bn}的前n项和T. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(x2﹣2ax)(a>0且a≠1)满足对任意的x1 , x2∈[3,4],且x1≠x2时,都有
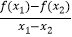 >0成立,则实数a的取值范围是
>0成立,则实数a的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式
 <0的解集为( )
<0的解集为( )
A.(﹣1,0)∪(1,+∞)
B.(﹣∞,﹣1)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,0)∪(0,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A(﹣4,a)作圆C的一条切线,切点为B,则|AB|=( )
A.2
B.6
C.4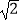
D.2
相关试题

