【题目】已知直线x+ay﹣1=0是圆C:x2+y2﹣4x﹣2y+1=0的对称轴,过点A(﹣4,a)作圆C的一条切线,切点为B,则|AB|=( )
A.2
B.6
C.4 ![]()
D.2 ![]()
参考答案:
【答案】B
【解析】解:∵圆C:x2+y2﹣4x﹣2y+1=0,即(x﹣2)2+(y﹣1)2 =4, 表示以C(2,1)为圆心、半径等于2的圆.
由题意可得,直线l:x+ay﹣1=0经过圆C的圆心(2,1),
故有2+a﹣1=0,∴a=﹣1,点A(﹣4,﹣1).
∵AC= ![]() =2
=2 ![]() ,CB=R=2,
,CB=R=2,
∴切线的长|AB|= ![]() =
= ![]() =6.
=6.
故选:B.
求出圆的标准方程可得圆心和半径,由直线l:x+ay﹣1=0经过圆C的圆心(2,1),求得a的值,可得点A的坐标,再利用直线和圆相切的性质求得|AB|的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 是椭圆
是椭圆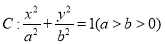 的左、右顶点,
的左、右顶点,  为左焦点,点
为左焦点,点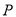 是椭圆上异于
是椭圆上异于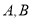 的任意一点,直线
的任意一点,直线 与过点
与过点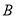 且垂直于
且垂直于 轴的直线
轴的直线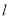 交于点
交于点 ,直线
,直线 于点
于点 .
.(1)求证:直线
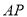 与直线
与直线 的斜率之积为定值;
的斜率之积为定值;(2)若直线
 过焦点
过焦点 ,
, 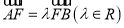 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(x2﹣2ax)(a>0且a≠1)满足对任意的x1 , x2∈[3,4],且x1≠x2时,都有
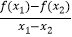 >0成立,则实数a的取值范围是
>0成立,则实数a的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式
 <0的解集为( )
<0的解集为( )
A.(﹣1,0)∪(1,+∞)
B.(﹣∞,﹣1)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,0)∪(0,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】圆心在直线x﹣2y=0上的圆C与y轴的正半轴相切,圆C截x轴所得弦的长为2
 ,求圆C的标准方程.
,求圆C的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣3x2+a(6﹣a)x+c.
(1)当c=19时,解关于a的不等式f(1)>0;
(2)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,c的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|0<ax+1≤5},B={x|﹣
 <x≤2}.
<x≤2}.
(1)当a=1时,判断集合BA是否成立?
(2)若AB,求实数a的取值范围.
相关试题

