【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如下图:记成绩不低于70分者为“成绩优良”.
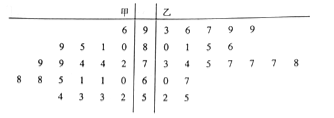
(1)分别计算甲、乙两班20个样本中,化学分数前十的平均分,并大致判断哪种教学方式的教学效果更佳;
(2)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附:![]()
独立性检验临界值表:
|
|
|
|
|
|
|
|
|
|
参考答案:
【答案】(1)![]() ,
,![]() ,“新课堂”的教学效果更佳;(2)列联表见解析,在犯错误的概率不超过
,“新课堂”的教学效果更佳;(2)列联表见解析,在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”.
的前提下认为“成绩优良与教学方式有关”.
【解析】
试题分析:根据茎叶图计算甲乙两班的化学成绩前十名学生的平均分即可;(2)填写列联表,计算![]() ,对照数表即可得出结论.
,对照数表即可得出结论.
试题解析:(1)甲班样本化学成绩前十的平均分为
![]()
![]() ;…………………………2分
;…………………………2分
乙班样本化学成绩前十的平均分为
![]() .………………………………4分
.………………………………4分
甲班样本化学成绩前十的平均分远低于乙班样本化学成绩前十的平均分,大致可以判断“高效课堂”教学方式的教学效果更佳.……………………………………………………6分
(2)
甲班( | 乙班( | 总计 | |
成绩优良 | 10 | 16 | 25 |
成绩不优良 | 10 | 4 | 14 |
总计 | 20 | 20 | 40 |
…………………………………………………………………………………………8分
根据![]() 列联表中的数据,得
列联表中的数据,得![]() 的观测值为
的观测值为![]() ,……10分
,……10分
∴能在犯错概率不超过![]() 的前提下认为“成绩优良与教学方式有关”.………………12分
的前提下认为“成绩优良与教学方式有关”.………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax3-
 x2+1(xR),其中a>0.
x2+1(xR),其中a>0. (1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若在区间
 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知右焦点为
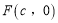 的椭圆
的椭圆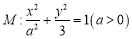 关于直线
关于直线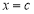 对称的图形过坐标原点.
对称的图形过坐标原点.(1)求椭圆
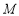 的方程;
的方程;(2)过点
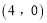 且不垂直于
且不垂直于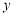 轴的直线与椭圆
轴的直线与椭圆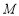 交于
交于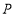 ,
,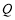 两点,点
两点,点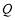 关于
关于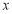 轴的对称点为
轴的对称点为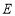 ,证明:直线
,证明:直线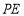 与
与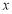 轴的交点为
轴的交点为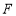 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
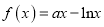 ,函数
,函数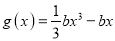 ,
, 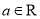 ,
, 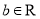 且
且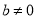 .
.(1)讨论函数
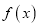 的单调性;
的单调性;(2)若
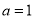 ,且对任意的
,且对任意的 ,总存在
,总存在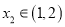 ,使
,使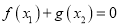 成立,求实数
成立,求实数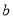 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,
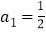 ,Sn=n2an-n(n-1),n=1,2,…
,Sn=n2an-n(n-1),n=1,2,…(1)证明:数列{
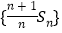 Sn}是等差数列,并求Sn;
Sn}是等差数列,并求Sn; (2)设
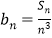 ,求证 :b1+b2+…+bn<1.
,求证 :b1+b2+…+bn<1. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为
 的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.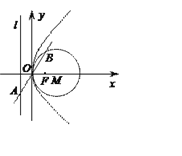
(1)求⊙M和抛物线C的方程;
(2)若P为抛物线C上的动点,求
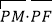 的最小值;
的最小值; (3)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,
初赛采用选手选一题答一题的方式进行,每位选手最多有
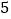 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对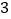 题或答错
题或答错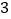 题即终止其初赛的比赛,答对
题即终止其初赛的比赛,答对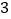 题者直接进入决赛,答错
题者直接进入决赛,答错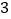 题者则被淘汰.已知选手甲答题的正确率为
题者则被淘汰.已知选手甲答题的正确率为 .
.(1) 求选手甲可进入决赛的概率;
(2) 设选手甲在初赛中答题的个数为
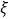 ,试写出
,试写出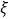 的分布列,并求
的分布列,并求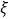 的数学期望.
的数学期望.
相关试题

