【题目】已知函数![]() ,函数
,函数![]() ,
, ![]() ,
, ![]() 且
且![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,且对任意的
,且对任意的![]() ,总存在
,总存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)当![]() 时,
时, ![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;(2)
上单调递增;(2)![]() .
.
【解析】试题分析:(1)确定函数定义域,对函数求导,根据导数的正负确定单调区间;(2)分别表示出![]() 的值域,根据
的值域,根据![]() 的值域应为
的值域应为![]() 的值域的子集可得答案.
的值域的子集可得答案.
试题解析:(1)![]() ,………………………………1分
,………………………………1分
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递减.……………………2分
上单调递减.……………………2分
当![]() 时,
时, ![]() 得
得![]() ;由
;由![]() 得
得![]() .…………………………4分
.…………………………4分
∴![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.………………5分
上单调递增.………………5分
(2)∵对任意的![]() ,总存在
,总存在![]() ,使
,使![]() ,
,
∴对任意的![]() ,总存在
,总存在![]() ,使
,使![]() ,………………6分
,………………6分
设![]() 在
在![]() 上的值域为
上的值域为![]() ,函数
,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,则
,则![]() .……7分
.……7分
当![]() 时,
时, ![]() ,即函数
,即函数![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,…………………………………………………………8分
,…………………………………………………………8分
![]() ,
,
①当![]() 时,
时, ![]() 在
在![]() 上是减函数,此时,
上是减函数,此时, ![]() 的值域为
的值域为![]() ,
,
∵![]() ,又
,又![]() ,∴
,∴![]() ,即
,即![]() .………………10分
.………………10分
②当![]() 时,
时, ![]() 在
在![]() 上是增函数,此时,
上是增函数,此时, ![]() 的值域为
的值域为![]() ,∵
,∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
综上可知![]() 的取值范围是
的取值范围是![]() .…………………………12分
.…………………………12分
-
科目: 来源: 题型:
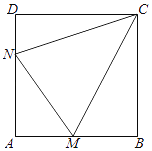
查看答案和解析>>【题目】如图所示,某村积极开展“美丽乡村生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上. (Ⅰ)当点M,N分别是边AB,AD的中点时,求∠MCN的余弦值;
(Ⅱ)由于村建规划及保护生态环境的需要,要求△AMN的周长为2千米,请探究∠MCN是否为定值,若是,求出此定值,若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax3-
 x2+1(xR),其中a>0.
x2+1(xR),其中a>0. (1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若在区间
 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知右焦点为
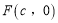 的椭圆
的椭圆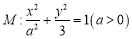 关于直线
关于直线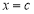 对称的图形过坐标原点.
对称的图形过坐标原点.(1)求椭圆
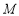 的方程;
的方程;(2)过点
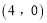 且不垂直于
且不垂直于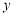 轴的直线与椭圆
轴的直线与椭圆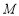 交于
交于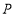 ,
,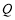 两点,点
两点,点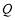 关于
关于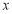 轴的对称点为
轴的对称点为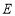 ,证明:直线
,证明:直线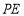 与
与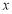 轴的交点为
轴的交点为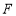 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如下图:记成绩不低于70分者为“成绩优良”.
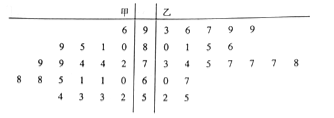
(1)分别计算甲、乙两班20个样本中,化学分数前十的平均分,并大致判断哪种教学方式的教学效果更佳;
(2)由以上统计数据填写下面
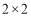 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过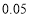 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?甲班
乙班
总计
成绩优良
成绩不优良
总计
附:
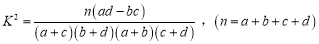
独立性检验临界值表:
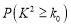
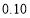
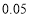
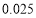
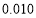
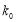

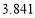
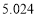
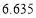
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,
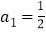 ,Sn=n2an-n(n-1),n=1,2,…
,Sn=n2an-n(n-1),n=1,2,…(1)证明:数列{
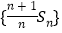 Sn}是等差数列,并求Sn;
Sn}是等差数列,并求Sn; (2)设
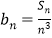 ,求证 :b1+b2+…+bn<1.
,求证 :b1+b2+…+bn<1. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为
 的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.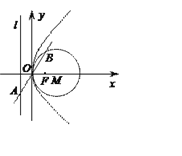
(1)求⊙M和抛物线C的方程;
(2)若P为抛物线C上的动点,求
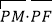 的最小值;
的最小值; (3)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
相关试题

