【题目】抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为![]() 的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
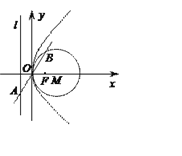
(1)求⊙M和抛物线C的方程;
(2)若P为抛物线C上的动点,求![]() 的最小值;
的最小值;
(3)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
参考答案:
【答案】(1)(x-2)2+y2=4。 (2)2.(3)![]() .
.
【解析】试题分析:(1)根据![]() 可求出
可求出![]() 的值,从而求出抛物线方程,求出圆心和半径可求出
的值,从而求出抛物线方程,求出圆心和半径可求出![]() 的方程;(2)先表示出
的方程;(2)先表示出![]() 然后根据点在抛物线上将
然后根据点在抛物线上将![]() 消去,求关于
消去,求关于![]() 的二次函数的最小值即可;(3)以点
的二次函数的最小值即可;(3)以点![]() 这圆心,
这圆心,![]() 为半径作
为半径作![]() ,则线段
,则线段![]() 即为
即为![]() 与
与![]() 的公共弦,设点
的公共弦,设点![]() ,根据
,根据![]() ,求出直线
,求出直线![]() 的方程,使直线与
的方程,使直线与![]() 无关,可求出定点坐标.
无关,可求出定点坐标.
试题解析:(1)因为=OA·cos60°=2×=1,即p=2,所以抛物线C的方程为y2=4x
设⊙M的半径为r,则r=![]() ·
·![]() =2,所以⊙M的方程为(x-2)2+y2=4。
=2,所以⊙M的方程为(x-2)2+y2=4。
(2)设P(x,y)(x≥0),则![]() ·
·![]() =(2-x,-y)(1-x,-y)=x2-3x+2+y2=x2+x+2,
=(2-x,-y)(1-x,-y)=x2-3x+2+y2=x2+x+2,
所以当x=0时,![]() ·
·![]() 有最小值为2.
有最小值为2.
(3)以点Q这圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦.
设点Q(-1,t),则QS2=QM2-4=t2+5,所以⊙Q的方程为(x+1)2+(y-t)2=t2+5,
从而直线QS的方程为3x-ty-2=0(*),
因为![]() 一定是方程(*)的解,所以直线QS恒过一个定点,且该定点坐标为(,0).
一定是方程(*)的解,所以直线QS恒过一个定点,且该定点坐标为(,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
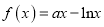 ,函数
,函数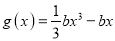 ,
, 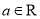 ,
, 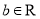 且
且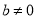 .
.(1)讨论函数
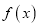 的单调性;
的单调性;(2)若
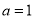 ,且对任意的
,且对任意的 ,总存在
,总存在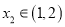 ,使
,使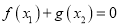 成立,求实数
成立,求实数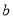 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如下图:记成绩不低于70分者为“成绩优良”.
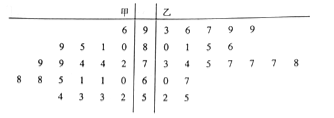
(1)分别计算甲、乙两班20个样本中,化学分数前十的平均分,并大致判断哪种教学方式的教学效果更佳;
(2)由以上统计数据填写下面
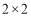 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过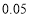 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?甲班
乙班
总计
成绩优良
成绩不优良
总计
附:
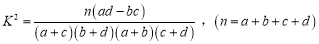
独立性检验临界值表:
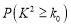
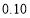
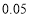
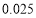
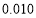
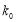

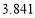
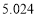
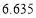
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,
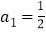 ,Sn=n2an-n(n-1),n=1,2,…
,Sn=n2an-n(n-1),n=1,2,…(1)证明:数列{
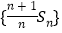 Sn}是等差数列,并求Sn;
Sn}是等差数列,并求Sn; (2)设
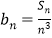 ,求证 :b1+b2+…+bn<1.
,求证 :b1+b2+…+bn<1. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,
初赛采用选手选一题答一题的方式进行,每位选手最多有
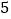 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对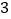 题或答错
题或答错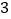 题即终止其初赛的比赛,答对
题即终止其初赛的比赛,答对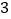 题者直接进入决赛,答错
题者直接进入决赛,答错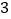 题者则被淘汰.已知选手甲答题的正确率为
题者则被淘汰.已知选手甲答题的正确率为 .
.(1) 求选手甲可进入决赛的概率;
(2) 设选手甲在初赛中答题的个数为
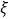 ,试写出
,试写出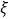 的分布列,并求
的分布列,并求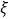 的数学期望.
的数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市决定在其经济开发区一块区域进行商业地产开发,截止2015年底共投资
 百万元用于餐饮业和服装业,2016年初正式营业,经过专业经济师预算,从2016年初至2019年底的四年间,在餐饮业利润为该业务投资额的
百万元用于餐饮业和服装业,2016年初正式营业,经过专业经济师预算,从2016年初至2019年底的四年间,在餐饮业利润为该业务投资额的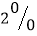 ,在服装业可获利该业务投资额的算术平方根.
,在服装业可获利该业务投资额的算术平方根.(1)该市投资资金应如何分配,才能使这四年总的预期利润最大?
(2)假设自2017年起,该市决定对所投资的区域设施进行维护保养,同时发放员工奖金,方案如下:2017年维护保养费用
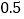 百万元,以后每年比上一年增加
百万元,以后每年比上一年增加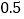 百万元;2017年发放员工奖金共计
百万元;2017年发放员工奖金共计 百万元,以后每年的奖金比上一年增加
百万元,以后每年的奖金比上一年增加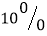 .若该市投资成功的标准是:从2016年初到2019的底,这四年总的预期利润中值(预期最大利润与最小利润的平均数)不低于总投资额的
.若该市投资成功的标准是:从2016年初到2019的底,这四年总的预期利润中值(预期最大利润与最小利润的平均数)不低于总投资额的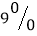 ,问该市投资是否成功?
,问该市投资是否成功? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人各进行3次射击,甲每次击中目标的概率为
 ,乙每次击中目标的概率为
,乙每次击中目标的概率为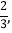 求:(1)甲恰好击中目标2次的概率;(2)乙至少击中目标2次的概率;
求:(1)甲恰好击中目标2次的概率;(2)乙至少击中目标2次的概率;(3)乙恰好比甲多击中目标2次的概率
相关试题

