【题目】已知函数![]() ,直线
,直线![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 有且仅有一个公共点,求公共点横坐标的值;
有且仅有一个公共点,求公共点横坐标的值;
(2)若![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(1)公共点的横坐标为![]() 和
和![]() ;(2)见解析
;(2)见解析
【解析】试题分析:
(1)利用题意分类讨论![]() 和
和![]() 可得公共点横坐标的值为
可得公共点横坐标的值为![]() 和
和![]() ;
;
(2)利用不等式的特点构造函数![]() ,结合新函数的特点和题意可得结论成立.
,结合新函数的特点和题意可得结论成立.
试题解析:
解:(1)由![]() ,得
,得![]() ,
,
易知![]() 时,
时, ![]() 单调递减,
单调递减, ![]() 时,
时, ![]() 单调递增,
单调递增,
根据直线![]() 的方程
的方程![]() ,可得
,可得![]() 恒过点
恒过点![]() ,
,
①当![]() 时,直线
时,直线![]() 垂直
垂直![]() 轴,与曲线
轴,与曲线![]() 相交于一点,即焦点横坐标为
相交于一点,即焦点横坐标为![]() ;
;
②当![]() 时,设切线
时,设切线![]() ,直线
,直线![]() 可化为
可化为![]() ,斜率
,斜率![]() ,
,
又直线![]() 和曲线
和曲线![]() 均过点
均过点![]() ,则满足
,则满足![]() ,
,
所以![]() ,两边约去
,两边约去![]() 后,
后,
可得![]() ,化简得
,化简得![]() ,
,
切点横坐标![]() ,综上所述,由①和②可知,该公共点的横坐标为
,综上所述,由①和②可知,该公共点的横坐标为![]() 和
和![]() ;
;
(2)①若![]() 时,欲证
时,欲证![]() ,
,
由题意![]() ,由问可知
,由问可知![]() 在
在![]() 上单调递减,证
上单调递减,证![]() 对
对![]() 恒成立即可.
恒成立即可.
设函数![]() ,则
,则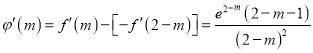 ,
,
即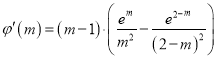 ,
,
设![]() ,则
,则![]() ,
,
易知![]() 时,
时, ![]() 单调递减,
单调递减, ![]() 时,
时, ![]() 单调递增,
单调递增,
当![]() 时,有
时,有![]() ,且满足
,且满足![]() ,故
,故![]() ,
,
即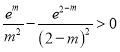 ,又
,又![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,有
上单调递减,有![]() ,
,
即![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知球内接四棱锥
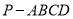 的高为
的高为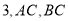 相交于
相交于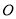 ,球的表面积为
,球的表面积为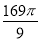 ,若
,若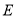 为
为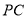 中点.
中点.(1)求异面直线
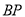 和
和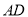 所成角的余弦值;
所成角的余弦值;(2)求点
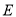 到平面
到平面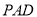 的距离.
的距离.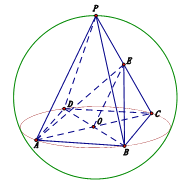
-
科目: 来源: 题型:
查看答案和解析>>【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足
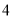 千步为不健康生活方式,不少于
千步为不健康生活方式,不少于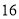 千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为
千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为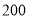 人,高一学生人数为
人,高一学生人数为 人,高二学生人数
人,高二学生人数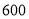 人,高三学生人数
人,高三学生人数 ,从中抽取
,从中抽取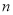 人作为调查对象,得到了如图所示的这
人作为调查对象,得到了如图所示的这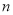 人的频率分布直方图,这
人的频率分布直方图,这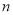 人中有
人中有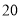 人被学校界定为不健康生活方式者.
人被学校界定为不健康生活方式者.(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取
 人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励
人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励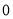 元,超健康生活方式者表彰奖励
元,超健康生活方式者表彰奖励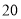 元,一般生活方式者鼓励性奖励
元,一般生活方式者鼓励性奖励 元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为
元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为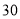 元的概率.
元的概率.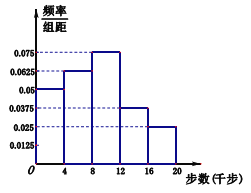
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如表:
零件的个数x(个)
2
3
4
5
加工的时间y(小时)
2.5
3
4
4.5
(1)求出y关于x的线性回归方程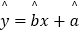 ;
;
(2)试预测加工10个零件需要多少小时?
(参考公式: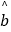 =
= 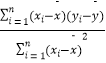 =
= 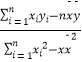 ;
;  ;)
;) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知球内接四棱锥
 的高为
的高为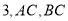 相交于
相交于 ,球的表面积为
,球的表面积为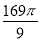 ,若
,若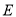 为
为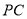 中点.
中点.(1)求证:
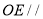 平面
平面 ;
;(2)求二面角
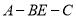 的余弦值.
的余弦值.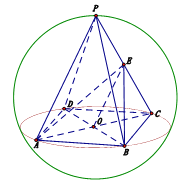
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点
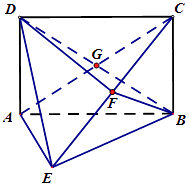
(1)求证:AE∥平面BFD
(2)求证:AE⊥平面BCE
(3)求三棱柱C﹣BGF的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论函数
 的单调性;
的单调性;(2)当
 时,若函数
时,若函数 的导函数
的导函数 的图象与
的图象与 轴交于
轴交于 ,
,  两点,其横坐标分别为
两点,其横坐标分别为 ,
,  ,线段
,线段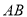 的中点的横坐标为
的中点的横坐标为 ,且
,且 ,
,  恰为函数
恰为函数 的零点,求证:
的零点,求证:  .
.
相关试题

