【题目】已知等比数列![]() 满足,
满足,![]() ,
,![]() .
.
![]() 求数列
求数列![]() 的通项公式;
的通项公式;
![]() 设
设![]() ,求
,求![]() 的前n项和为
的前n项和为![]() .
.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)根据等比数列的首项和公比求通项公式;一般转化为首项和公比列方程求解,注意题中限制条件;(2)先求{![]() }的通项公式然后再求和,除此外还会有观察数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.(3)在做题时注意观察式子特点选择有关公式和性质进行化简,这样给做题带来方便,掌握常见求和方法,如分组转化求和,裂项法,错位相减.
}的通项公式然后再求和,除此外还会有观察数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.(3)在做题时注意观察式子特点选择有关公式和性质进行化简,这样给做题带来方便,掌握常见求和方法,如分组转化求和,裂项法,错位相减.
试题解析:1)设数列{![]() }的首项为
}的首项为![]() ,公比为
,公比为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]()
(2)因为![]() ,所以数列{
,所以数列{![]() }的前
}的前![]() 项和
项和![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】雾霾大气严重影响人们的生活,某科技公司拟投资开发新型节能环保产品,策划部制定投资计划时,不仅要考虑可能获得的盈利,而且还要考虑可能出现的亏损,经过市场调查,公司打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为
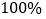 和
和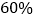 ,可能的最大亏损率分别为
,可能的最大亏损率分别为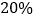 和
和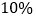 ,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过
,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过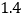 万元.
万元. Ⅰ
Ⅰ 若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形.
若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形. Ⅱ
Ⅱ 根据
根据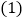 的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?
的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx的图象上有A、B两点,其横坐标为x1 , x2(0<x1<x2<1)且满足f(x1)=f(x2),若k=5(
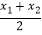 +
+ 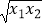 ),且k为整数时,则k的值为( )(参考数据:e≈2.72)
),且k为整数时,则k的值为( )(参考数据:e≈2.72)
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,
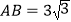 ,
,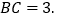 沿对角线将
沿对角线将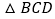 折起,使点C移到
折起,使点C移到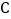 点,且C点在平面ABD的射影O恰在AB上.
点,且C点在平面ABD的射影O恰在AB上.(1)求证:
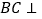 平面ACD;
平面ACD;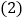 求直线AB与平面
求直线AB与平面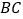 D所成角的正弦值.
D所成角的正弦值.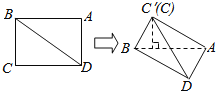
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
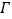 :
: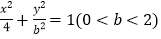 的左右焦点分别为
的左右焦点分别为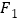 、
、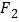 ,上顶点为B,O为坐标原点,且向量
,上顶点为B,O为坐标原点,且向量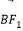 与
与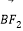 的夹角为
的夹角为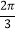 .
.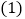 求椭圆
求椭圆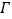 的方程;
的方程;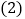 设
设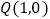 ,点P是椭圆
,点P是椭圆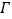 上的动点,求
上的动点,求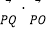 的最大值和最小值;
的最大值和最小值; 设不经过点B的直线l与椭圆
设不经过点B的直线l与椭圆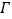 相交于M、N两点,且直线BM、BN的斜率之和为1,证明:直线l过定点.
相交于M、N两点,且直线BM、BN的斜率之和为1,证明:直线l过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
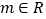 ,命题
,命题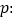 方程
方程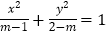 表示焦点在
表示焦点在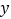 轴上的椭圆,命题
轴上的椭圆,命题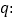 方程
方程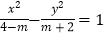 表示双曲线.
表示双曲线.(1)若命题
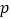 是真命题,求实数
是真命题,求实数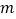 的范围;
的范围;(2)若命题“
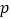 或
或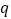 ”为真命题,“
”为真命题,“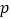 且
且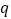 ”是假命题,求实数
”是假命题,求实数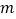 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是自动通风设施
 该设施的下部ABCD是等腰梯形,其中
该设施的下部ABCD是等腰梯形,其中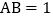 米,高
米,高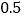 米,
米,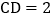 米
米 上部CmD是个半圆,固定点E为CD的中点
上部CmD是个半圆,固定点E为CD的中点 是由电脑控制其形状变化的三角通风窗
是由电脑控制其形状变化的三角通风窗 阴影部分均不通风
阴影部分均不通风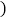 ,MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
,MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.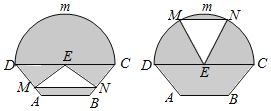
 设MN与AB之间的距离为x米,试将三角通风窗
设MN与AB之间的距离为x米,试将三角通风窗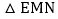 的通风面积
的通风面积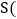 平方米
平方米 表示成关于x的函数
表示成关于x的函数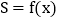 ;
;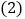 当MN与AB之间的距离为多少米时,三角通风窗
当MN与AB之间的距离为多少米时,三角通风窗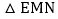 的通风面积最大?求出这个最大面积.
的通风面积最大?求出这个最大面积.
相关试题

