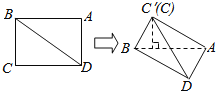
【题目】如图所示,在矩形ABCD中,![]() ,
,![]() 沿对角线将
沿对角线将![]() 折起,使点C移到
折起,使点C移到![]() 点,且C点在平面ABD的射影O恰在AB上.
点,且C点在平面ABD的射影O恰在AB上.
(1)求证:![]() 平面ACD;
平面ACD;
![]() 求直线AB与平面
求直线AB与平面![]() D所成角的正弦值.
D所成角的正弦值.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由已知条件推导出DA⊥BC,BC⊥DC,由此能证明BC⊥平面ACD.
(2)作AM⊥DC于M,由已知条件推导出∠ABM是AB与平面BCD所成的角,由此能求出直线AB与平面BCD所成角的正弦值.
![]() 证明:
证明:![]() 在矩形ABCD中,
在矩形ABCD中,![]() ,
,
![]() 平面ABD,AB是BC在平面ABD内的射影,
平面ABD,AB是BC在平面ABD内的射影,
![]() ,
,![]() ,
,
又![]() ,
,![]() 平面ACD.
平面ACD.
![]() 解:作
解:作![]() 于M,连接BM,
于M,连接BM,
![]() ,
,![]() ,
,![]() 平面ADC,
平面ADC,
![]() 平面SDC,
平面SDC,![]() 平面
平面![]() 平面BDC,
平面BDC,
又![]() ,
,![]() 平面
平面![]() 平面BDC,
平面BDC,
所以![]() 平面BCD,
平面BCD,
所以![]() 是AB与平面BCD所成的角,
是AB与平面BCD所成的角,
在![]() 中,
中,![]() ,
,![]() ,
,
在![]() 中,
中,![]() .
.
![]() 直线AB与平面BCD所成角的正弦值为
直线AB与平面BCD所成角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足
 ,则使不等式a2016>2017成立的所有正整数a1的集合为( )
,则使不等式a2016>2017成立的所有正整数a1的集合为( )
A.{a1|a1≥2017,a1∈N+}
B.{a1|a1≥2016,a1∈N+}
C.{a1|a1≥2015,a1∈N+}
D.{a1|a1≥2014,a1∈N+} -
科目: 来源: 题型:
查看答案和解析>>【题目】雾霾大气严重影响人们的生活,某科技公司拟投资开发新型节能环保产品,策划部制定投资计划时,不仅要考虑可能获得的盈利,而且还要考虑可能出现的亏损,经过市场调查,公司打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为
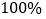 和
和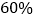 ,可能的最大亏损率分别为
,可能的最大亏损率分别为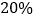 和
和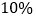 ,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过
,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过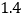 万元.
万元. Ⅰ
Ⅰ 若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形.
若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形. Ⅱ
Ⅱ 根据
根据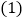 的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?
的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?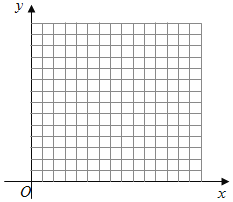
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx的图象上有A、B两点,其横坐标为x1 , x2(0<x1<x2<1)且满足f(x1)=f(x2),若k=5(
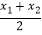 +
+ 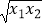 ),且k为整数时,则k的值为( )(参考数据:e≈2.72)
),且k为整数时,则k的值为( )(参考数据:e≈2.72)
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列
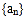 满足,
满足,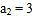 ,
,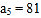 .
. 求数列
求数列 的通项公式;
的通项公式; 设
设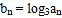 ,求
,求 的前n项和为
的前n项和为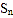 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
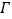 :
: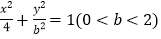 的左右焦点分别为
的左右焦点分别为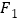 、
、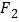 ,上顶点为B,O为坐标原点,且向量
,上顶点为B,O为坐标原点,且向量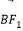 与
与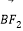 的夹角为
的夹角为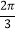 .
. 求椭圆
求椭圆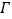 的方程;
的方程; 设
设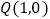 ,点P是椭圆
,点P是椭圆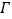 上的动点,求
上的动点,求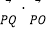 的最大值和最小值;
的最大值和最小值; 设不经过点B的直线l与椭圆
设不经过点B的直线l与椭圆 相交于M、N两点,且直线BM、BN的斜率之和为1,证明:直线l过定点.
相交于M、N两点,且直线BM、BN的斜率之和为1,证明:直线l过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
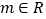 ,命题
,命题 方程
方程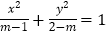 表示焦点在
表示焦点在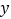 轴上的椭圆,命题
轴上的椭圆,命题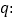 方程
方程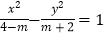 表示双曲线.
表示双曲线.(1)若命题
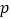 是真命题,求实数
是真命题,求实数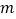 的范围;
的范围;(2)若命题“
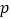 或
或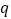 ”为真命题,“
”为真命题,“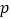 且
且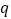 ”是假命题,求实数
”是假命题,求实数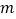 的范围.
的范围.
相关试题

