【题目】某河上有座抛物线型拱桥,当水面距拱顶5m时水面宽为8m,一木船宽为4m,高为2m,载货后木船露在水面上的部分高为0.75m,问水面上涨到与拱顶相距多少时,木船开始不能通过。
参考答案:
【答案】水面上涨到与抛物线拱顶距2米时,小船开始不能通行
【解析】
试题分析:建立平面直角坐标系,设拱桥型抛物线方程为x2=-2py(p>0).将B(4,-5)代入得p=1.6,所以x2=-3.2y,当船两侧与抛物线接触时不能通过,由此能求出结果
试题解析:建立平面直角坐标系,

设拱桥型抛物线方程为x2=-2py(p>0).…(2分)
将B(4,-5)代入得p=1.6,
∴x2=-3.2y,…(6分)
当船两侧与抛物线接触时不能通过,
设点A(2,yA),
由22=-3.2 yA,
得yA =-1.25,…(10分)
因为船露出水面的部分高0.75米,…(12分)
所以h=|yA|+0.75=2米.…(14分)
答:水面上涨到与抛物线拱顶距2米时,小船开始不能通行.…(16分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线C的顶点在x轴上,两顶点间的距离是8,离心率

(1)求双曲线C的标准方程;
(2)过点P(3,0)且斜率为k的直线与双曲线C有且仅有一个公共点,求k的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
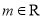 ,直线
,直线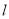 :
: 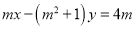 和圆
和圆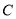 :
:  .
.(Ⅰ)求直线
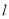 斜率的取值范围;
斜率的取值范围;(Ⅱ)直线
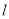 能否将圆
能否将圆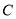 分割成弧长的比值为
分割成弧长的比值为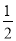 的两段圆弧?为什么?
的两段圆弧?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
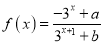 .
.(1)当
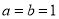 时,求满足
时,求满足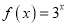 的
的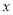 的取值;
的取值;(2)若函数
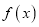 是定义在
是定义在 上的奇函数
上的奇函数①存在
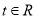 ,不等式
,不等式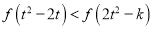 有解,求
有解,求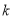 的取值范围;
的取值范围;②若函数
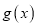 满足
满足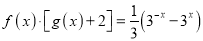 ,若对任意
,若对任意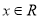 ,不等式
,不等式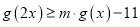 恒成立,求实数
恒成立,求实数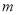 的最大值.
的最大值. -
科目: 来源: 题型:
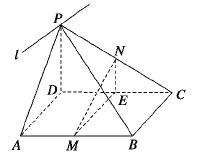
查看答案和解析>>【题目】如图,P为平行四边形ABCD所在平面外一点,MN分别为ABPC的中点,平面PAD∩平面PBC=l.
(1)判断BC与l的位置关系,并证明你的结论;
(2)判断MN与平面PAD的位置关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥
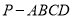 中,点
中,点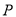 在平面
在平面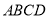 内的射影
内的射影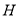 在棱
在棱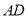 上,
上,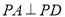 ,底面
,底面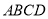 是梯形,
是梯形,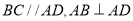 ,且
,且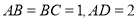 .
.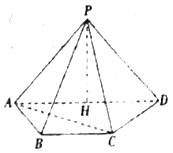
(1)求证:平面
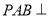 平面
平面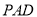 ;
;(2)若直线
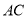 与
与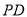 所成角为60°,求二面角
所成角为60°,求二面角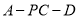 的余弦值.
的余弦值. -
科目: 来源: 题型:
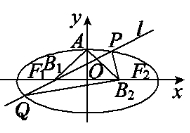
查看答案和解析>>【题目】如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程__________.
相关试题

