【题目】已知![]() ,直线
,直线![]() :
: ![]() 和圆
和圆![]() :
: ![]() .
.
(Ⅰ)求直线![]() 斜率的取值范围;
斜率的取值范围;
(Ⅱ)直线![]() 能否将圆
能否将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段圆弧?为什么?
的两段圆弧?为什么?
参考答案:
【答案】(1)![]() (2)不能.
(2)不能.
【解析】试题分析:(Ⅰ)由直线方程的一般式可得直线的斜率![]() ,利用不等式性质可求出
,利用不等式性质可求出![]() 的取值范围;(Ⅱ)利用点到直线的距离可求出圆心到直线的距离为
的取值范围;(Ⅱ)利用点到直线的距离可求出圆心到直线的距离为![]() ,再利用
,再利用![]() 的范围得出,此距离大于半径的一半,结合图形知直线与圆若相交,所对的圆心角小于
的范围得出,此距离大于半径的一半,结合图形知直线与圆若相交,所对的圆心角小于![]() ,可得结论.
,可得结论.
试题解析:(Ⅰ)直线![]() 的方程可化为
的方程可化为![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
因为![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
所以,斜率![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)不能.由(Ⅰ)即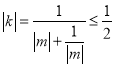 .圆
.圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() .
.
圆心![]() 到直线
到直线![]() 的距离
的距离![]() .由
.由![]() ,得
,得![]() ,即
,即![]() .
.
从而,若![]() 与圆
与圆![]() 相交,则圆
相交,则圆![]() 截直线
截直线![]() 所得的弦所对的圆心角小于
所得的弦所对的圆心角小于![]() .
.
所以![]() 不能将圆
不能将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段弧.
的两段弧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0,分别求满足下列条件的a,b值
(1)l1⊥l2,且直线l1过点(﹣3,﹣1);
(2)l1∥l2,且直线l1在两坐标轴上的截距相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),则实数x的取值范围为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线C的顶点在x轴上,两顶点间的距离是8,离心率

(1)求双曲线C的标准方程;
(2)过点P(3,0)且斜率为k的直线与双曲线C有且仅有一个公共点,求k的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
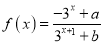 .
.(1)当
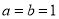 时,求满足
时,求满足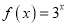 的
的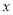 的取值;
的取值;(2)若函数
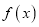 是定义在
是定义在 上的奇函数
上的奇函数①存在
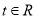 ,不等式
,不等式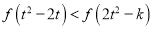 有解,求
有解,求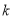 的取值范围;
的取值范围;②若函数
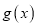 满足
满足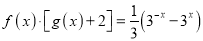 ,若对任意
,若对任意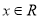 ,不等式
,不等式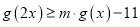 恒成立,求实数
恒成立,求实数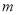 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某河上有座抛物线型拱桥,当水面距拱顶5m时水面宽为8m,一木船宽为4m,高为2m,载货后木船露在水面上的部分高为0.75m,问水面上涨到与拱顶相距多少时,木船开始不能通过。
-
科目: 来源: 题型:
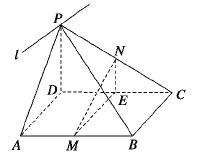
查看答案和解析>>【题目】如图,P为平行四边形ABCD所在平面外一点,MN分别为ABPC的中点,平面PAD∩平面PBC=l.
(1)判断BC与l的位置关系,并证明你的结论;
(2)判断MN与平面PAD的位置关系,并证明你的结论.
相关试题

