【题目】已知函数f(x)=ax3+x2(a∈R)在x=﹣![]() 处取得极值.
处取得极值.
(1)确定a的值;
(2)讨论函数g(x)=f(x)ex的单调性.
参考答案:
【答案】(1) a=![]() ;(2) 在(﹣∞,﹣4)和(﹣1,0)内为减函数,在(﹣4,﹣1)和(0,+∞)为增函数.
;(2) 在(﹣∞,﹣4)和(﹣1,0)内为减函数,在(﹣4,﹣1)和(0,+∞)为增函数.
【解析】(1)对f(x)求导得f′(x)=3ax2+2x.
∵f(x)=ax3+x2(a∈R)在x=﹣![]() 处取得极值,∴f′(﹣
处取得极值,∴f′(﹣![]() )=0,
)=0,
∴3a![]() +2(﹣
+2(﹣![]() )=0,∴a=
)=0,∴a=![]() ;
;
(2)由(1)得g(x)=(![]() x3+x2)ex,
x3+x2)ex,
∴g′(x)=(![]() x2+2x)ex+(
x2+2x)ex+(![]() x3+x2)ex=
x3+x2)ex=![]() x(x+1)(x+4)ex,
x(x+1)(x+4)ex,
令g′(x)=0,解得x=0,x=﹣1或x=﹣4,
当x<﹣4时,g′(x)<0,故g(x)为减函数;
当﹣4<x<﹣1时,g′(x)>0,故g(x)为增函数;
当﹣1<x<0时,g′(x)<0,故g(x)为减函数;
当x>0时,g′(x)>0,故g(x)为增函数;
综上知g(x)在(﹣∞,﹣4)和(﹣1,0)内为减函数,在(﹣4,﹣1)和(0,+∞)为增函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
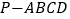 中,底面
中,底面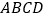 是边长为2的正方形,
是边长为2的正方形,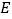 ,
,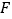 分别为
分别为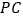 ,
,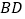 的中点,平面
的中点,平面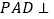 平面
平面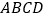 ,且
,且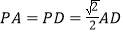 .
.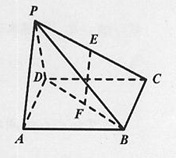
(1)求证:
 平面
平面 ;
;(2)求三棱锥
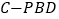 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
甲
82
82
79
95
87
乙
95
75
80
90
85
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
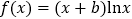 ,已知曲线
,已知曲线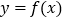 在点
在点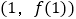 处的切线与直线
处的切线与直线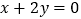 垂直.
垂直.(1)求
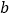 的值;
的值;(2)若函数
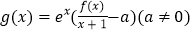 ,且
,且 在区间
在区间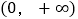 上是单调函数,求实数
上是单调函数,求实数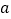 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=
 ﹣p
﹣p④回归直线一定过样本点的中心(
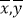 ).
).其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间20名工人年龄数据如下表:
年龄(岁)
19
24
26
30
34
35
40
合计
工人数(人)
1
3
3
5
4
3
1
20
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
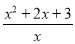 ,其中x∈[2,+∞).
,其中x∈[2,+∞).(1)求f(x)的最小值;
(2)若f(x)>a恒成立,求a的取值范围.
相关试题

