【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,点
,点 在椭圆
在椭圆![]() 上,直线
上,直线![]() 过椭圆的右焦点
过椭圆的右焦点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点.
两点.
(1)求![]() 的方程;
的方程;
(2)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出定点
为定值?若存在,求出定点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
参考答案:
【答案】(1)![]() (2)存在定点
(2)存在定点![]() ,使得
,使得![]() 为定值
为定值![]()
【解析】试题分析:(1)由题意的离心率公式求得![]() ,将
,将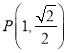 代入椭圆方程,即可求得
代入椭圆方程,即可求得![]() 和
和![]() ,从而可得椭圆方程;(2)在
,从而可得椭圆方程;(2)在![]() 轴上假设存在定点
轴上假设存在定点![]() ,使得
,使得![]() 为定值,若直线的斜率存在,设
为定值,若直线的斜率存在,设![]() 的科率为
的科率为![]() ,由
,由![]() 代入椭圆方程,运用韦达定理和向量数量积的坐标表示,结合恒成立思想,即可得到定点和定值;检验直线
代入椭圆方程,运用韦达定理和向量数量积的坐标表示,结合恒成立思想,即可得到定点和定值;检验直线![]() 的斜率不存在时,也成立.
的斜率不存在时,也成立.
试题解析:(1)由![]() ,
, 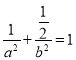 ,解出
,解出![]() 可得椭圆
可得椭圆![]() 的方程为
的方程为![]() .
.
(2)由直线![]() 过椭圆右焦点
过椭圆右焦点![]() ,
,
当直线![]() 不与
不与![]() 轴重合时,可设
轴重合时,可设![]()
代入椭圆方程,并整理得![]()
设![]() ,
, ![]() ,则
,则![]() ,
, ![]()
设![]() ,则
,则![]()
![]()
![]()
![]() 为定值,
为定值,
则![]() ,解得
,解得![]()
故存在定点![]() ,使得
,使得![]() 为定值
为定值![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和数量积公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
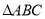 不是直角三角形,它的三个角
不是直角三角形,它的三个角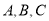 所对的边分别为
所对的边分别为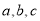 ,已知
,已知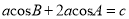 .
.(1)求证:
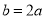 ;
;(2)如果
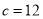 ,求
,求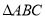 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位计划在一水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量
 (年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.(1)求未来3年中,设
 表示流量超过120的年数,求
表示流量超过120的年数,求 的分布列及期望;
的分布列及期望;(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量
 限制,并有如下关系:
限制,并有如下关系:年入流量




发电机最多可运行台数
1
2
3
若某台发电机运行,则该台年利润为5000万元,若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 ,
, 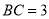 ,过动点A作
,过动点A作 ,垂足D在线段BC上且异于点B,连接AB,沿
,垂足D在线段BC上且异于点B,连接AB,沿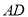 将△
将△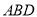 折起,使
折起,使 (如图2所示).
(如图2所示).
(1)当
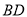 的长为多少时,三棱锥
的长为多少时,三棱锥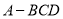 的体积最大;
的体积最大;(2)当三棱锥
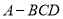 的体积最大时,设点
的体积最大时,设点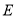 ,
, 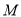 分别为棱
分别为棱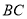 ,
, 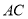 的中点,试在棱
的中点,试在棱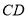 上确定一点
上确定一点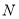 ,使得
,使得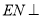
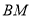 ,并求
,并求 与平面
与平面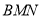 所成角的大小.
所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(1)求函数
 的单调区间;
的单调区间;(2)若不等式
 区间
区间 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;(3)求证:

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标
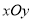 中,圆
中,圆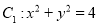 ,圆
,圆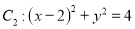 。
。(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆
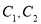 的极坐标方程,并求出圆
的极坐标方程,并求出圆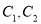 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);(Ⅱ)求圆
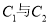 的公共弦的参数方程。
的公共弦的参数方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意
 ,
,  有唯一确定的
有唯一确定的 与之对应,则称
与之对应,则称 为关于
为关于 ,
,  的二元函数,现定义满足下列性质的
的二元函数,现定义满足下列性质的 为关于实数
为关于实数 ,
,  的广义“距离”.
的广义“距离”.(
 )非负性:
)非负性:  ,当且仅当
,当且仅当 时取等号;
时取等号;(
 )对称性:
)对称性:  ;
;(
 )三角形不等式:
)三角形不等式:  对任意的实数
对任意的实数 均成立.
均成立.给出三个二元函数:①
 ;②
;② ;③
;③ ,
,则所有能够成为关于
 ,
,  的广义“距离”的序号为__________.
的广义“距离”的序号为__________.
相关试题

