【题目】某玩具所需成本费用为P元,且P=1 000+5x+![]() x2,而每套售出的价格为Q元,其中Q(x)=a+
x2,而每套售出的价格为Q元,其中Q(x)=a+![]() (a,b∈R),
(a,b∈R),
(1)问:玩具厂生产多少套时,使得每套所需成本费用最少?
(2)若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求a,b的值.(利润=销售收入-成本).
参考答案:
【答案】(1)该玩具厂生产100套时每套所需成本最少.(2)a=25,b=30.
【解析】
(1)先建立每套所需成本费用函数关系式,再根据基本不等式求最值,(2)先根据利润=销售收入-成本建立利润函数关系式,再根据二次函数性质确定开口方向、对称轴位置以及最大值取法,解方程与不等式组可得a,b的值.
解:(1)每套玩具所需成本费用为![]() =
=![]()
=![]() x+
x+![]() +5≥2
+5≥2![]() +5=25,
+5=25,
当![]() x=
x=![]() ,即x=100时等号成立,
,即x=100时等号成立,
故该玩具厂生产100套时每套所需成本最少.
(2)设售出利润为w,则w=x·Q(x)-P
=x![]() -
-![]()
=![]() x2+(a-5)x-1 000,
x2+(a-5)x-1 000,
由题意得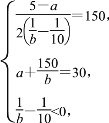 解得a=25,b=30.
解得a=25,b=30.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校有两个参加国际中学生交流活动的代表名额,为此该学校高中部推荐2男1女三名候选人,初中部也推荐了1男2女三名候选人。若从6名学生中人选2人做代表。
求:(1)选出的2名同学来自不同年相级部且性别同的概率;
(2)选出的2名同学都来自高中部或都来自初中部的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】 在平行四边形ABCD中,A(1,1),
 =(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若
=(6,0),点M是线段AB的中点,线段CM与BD交于点P.(1) 若 =(3,5),求点C的坐标;(2) 当|
=(3,5),求点C的坐标;(2) 当| |=|
|=| |时,求点P的轨迹.
|时,求点P的轨迹. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,直线
,直线 交此抛物线于不同的两个点
交此抛物线于不同的两个点 、
、 .
.(
 )当直线
)当直线 过点
过点 时,证明
时,证明 ,
, 为定值.
为定值.(
 )当
)当 时,直线
时,直线 是否过定点?若过定点,求出定点坐标;反之,请说明理由.
是否过定点?若过定点,求出定点坐标;反之,请说明理由.(
 )记
)记 ,如果直线
,如果直线 过点
过点 ,设线段
,设线段 的中点为
的中点为 ,线段
,线段 的中点为
的中点为 .问是否存在一条直线和一个定点,使得点
.问是否存在一条直线和一个定点,使得点 到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.
到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中, ,
, 为线段
为线段 的中点,
的中点, 为线段
为线段 上一点.
上一点.
(1)求证:
 ;
;(2)求证:平面
 平面
平面 ;
;(3)当
 平面
平面 时,求三棱锥
时,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】用空间向量解决下列问题:如图,在斜三棱柱
 中,
中,  是
是 的中点,
的中点,  ⊥平面
⊥平面 ,
,  ,
,  .
.
(1)求证:
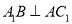 ;
;(2)求二面角
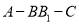 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ,
,(1)求不等式
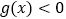 的解集;
的解集;(2)若对一切
 ,均有
,均有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
相关试题

