【题目】设椭圆![]() 的焦点
的焦点![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,若
两点,若![]() 的周长为短轴长的
的周长为短轴长的![]() 倍.
倍.
(1)求![]() 的离心率;
的离心率;
(2)设![]() 的斜率为
的斜率为![]() ,在
,在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标; 若不存在,说明理由.
的坐标; 若不存在,说明理由.
参考答案:
【答案】(1)![]() (2)不存在
(2)不存在
【解析】
试题分析:(1)求椭圆离心率,只需建立一个等量关系即可:因为![]() 的周长为
的周长为![]() ,所以
,所以![]() ,注意短轴长为
,注意短轴长为![]() ,即可得到
,即可得到![]() (2)存在性问题,以算代证,有解就存在,无解就不存在. 设
(2)存在性问题,以算代证,有解就存在,无解就不存在. 设![]() ,
,![]() ,则
,则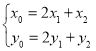 ,代入椭圆方程为
,代入椭圆方程为![]() 化简得
化简得![]() ,再根据直线方程
,再根据直线方程![]() 与椭圆方程联立方程组,利用韦达定理得
与椭圆方程联立方程组,利用韦达定理得![]() ,计算
,计算 ![]() ,则与
,则与![]() 矛盾,故不存在
矛盾,故不存在
试题解析:(1)![]() 的周长为
的周长为![]() ,依题意知
,依题意知![]() ,即
,即  .
.
(2)设椭圆方程为![]() ,直线的方程为
,直线的方程为![]() ,代入椭圆方程得
,代入椭圆方程得![]() ,
,
设![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ①
①
由![]() 得
得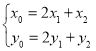 ,代入① 得
,代入① 得![]() ,
,
因为![]() ②
②
而![]() ,从而 ②式不成立. 故不存在点
,从而 ②式不成立. 故不存在点![]() ,使
,使![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
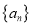 的前
的前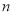 项和为
项和为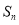 ,
,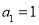 ,
,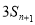 是6与
是6与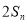 的等差中项
的等差中项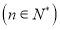 .
.(1)求数列
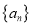 的通项公式;
的通项公式;(2)是否存在正整数
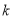 ,使不等式
,使不等式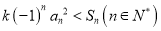 恒成立,若存在,求出
恒成立,若存在,求出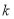 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
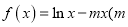 为常数).
为常数).(1)讨论函数
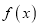 的单调性;
的单调性; (2)当
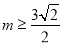 时,设
时,设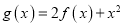 的两个极值点
的两个极值点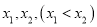 恰为
恰为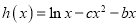 的零点,求
的零点,求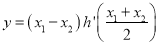 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了在冬季供暖时减少能量损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用
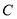 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度 (单位:
(单位: )满足关系:
)满足关系: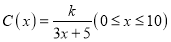 ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设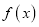 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.(1)求
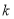 的值及
的值及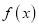 的表达式;
的表达式;(2)隔热层修建多厚时,总费用
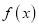 达到最小,并求最小值.
达到最小,并求最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱柱
 中,底面
中,底面 是菱形,且
是菱形,且 .
.(1) 求证: 平面
 平面
平面 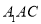 ;
;(2)若
 ,求平面
,求平面 与平面
与平面 所成角的大小.
所成角的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克).

规定:当食品中的有害微量元素的含量在
 时为一等品,在
时为一等品,在 为二等品,20以上为劣质品.
为二等品,20以上为劣质品.(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个,求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元,根据上表统计得到甲、乙两种食品为一等品、二等品、劣质品的频率,分别估计这两种食品为一等品、二等品、劣质品的概率,若分别从甲、乙食品中各抽取1件,设这两件食品给该厂带来的盈利为
 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品
 和产品
和产品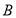 需要甲、乙两种新型材料,生产一件产品
需要甲、乙两种新型材料,生产一件产品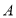 需要甲材料1.5
需要甲材料1.5 ,乙材料1
,乙材料1 ,用5个工时,生产一件产品需要甲材料0.5
,用5个工时,生产一件产品需要甲材料0.5 ,乙材料0.3
,乙材料0.3 ,用3个工时,生产一件产品的利润为2100元,生产一件产品的利润为900元.该企业现有甲材料150
,用3个工时,生产一件产品的利润为2100元,生产一件产品的利润为900元.该企业现有甲材料150 ,乙材料90
,乙材料90 ,则在不超过600个工时的条件下,生产产品
,则在不超过600个工时的条件下,生产产品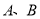 的利润之和的最大值为____________元.
的利润之和的最大值为____________元.
相关试题

