【题目】已知函数![]() 为常数).
为常数).
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,设
时,设![]() 的两个极值点
的两个极值点![]() 恰为
恰为![]() 的零点,求
的零点,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间减区间为
,单调递减区间减区间为![]() ,当
,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() .(2)
.(2)![]()
【解析】
试题分析:(1)先求函数导数![]() ,讨论导函数符号变化规律:当
,讨论导函数符号变化规律:当![]() 时,导函数不变号,故
时,导函数不变号,故![]() 的单调递增区间为
的单调递增区间为![]() .当
.当![]() 时,导函数符号由正变负,即单调递增区间为
时,导函数符号由正变负,即单调递增区间为![]() ,单调递减区间减区间为
,单调递减区间减区间为![]() ,(2)先求
,(2)先求![]() 导数得
导数得![]() 为方程
为方程![]() 的两根,再求
的两根,再求![]() 导数得
导数得![]() ,因此
,因此![]() ,而由
,而由![]() 为
为![]() 的零点,得
的零点,得![]() ,两式相减得
,两式相减得![]() ,即得
,即得![]() ,因此
,因此![]() ,从而
,从而![]()

![]() ,其中
,其中![]() 根据韦达定理确定自变量范围:因为
根据韦达定理确定自变量范围:因为![]()
又 ,所以
,所以![]()
试题解析:(1)![]() ,当
,当![]() 时,由
时,由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() 单调递增, 由
单调递增, 由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() 故
故![]() ,即
,即![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间减区间为
,单调递减区间减区间为![]() ,当
,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)![]() ,则
,则![]() ,所以
,所以![]() 的两根
的两根![]() 即为方程
即为方程![]() 的两根. 因为
的两根. 因为![]() ,所以
,所以![]() ,又因为
,又因为![]() 为
为![]() 的零点,所以
的零点,所以![]() ,两式相减得
,两式相减得![]() ,得
,得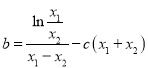 ,而
,而![]() ,
,
所以
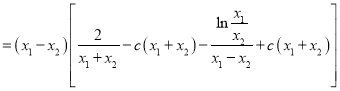

令![]() ,由
,由![]() 得
得![]()
因为![]() ,两边同时除以
,两边同时除以![]() ,得
,得![]() ,因为
,因为![]() ,故
,故![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ,设
,设![]() ,所以
,所以 ,则
,则![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,即
,即![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱
 中,已知
中,已知 ,
, 分别为
分别为 ,
, 的中点,点
的中点,点 在棱
在棱 上,且
上,且 .求证:
.求证:(1)直线
 ∥平面
∥平面 ;
;(2)直线
 平面
平面 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,已知圆
中,已知圆 及点
及点 ,
, .
.(1)若直线
 平行于
平行于 ,与圆
,与圆 相交于
相交于 ,
, 两点,
两点, ,求直线
,求直线 的方程;
的方程;(2)在圆
 上是否存在点
上是否存在点 ,使得
,使得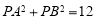 ?若存在,求点
?若存在,求点 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
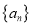 的前
的前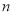 项和为
项和为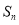 ,
,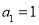 ,
,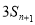 是6与
是6与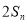 的等差中项
的等差中项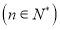 .
.(1)求数列
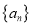 的通项公式;
的通项公式;(2)是否存在正整数
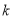 ,使不等式
,使不等式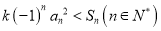 恒成立,若存在,求出
恒成立,若存在,求出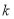 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了在冬季供暖时减少能量损耗,房屋的屋顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用
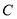 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度 (单位:
(单位: )满足关系:
)满足关系: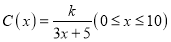 ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设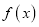 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.(1)求
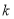 的值及
的值及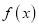 的表达式;
的表达式;(2)隔热层修建多厚时,总费用
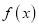 达到最小,并求最小值.
达到最小,并求最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
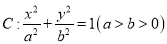 的焦点
的焦点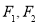 ,过右焦点
,过右焦点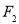 的直线
的直线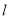 与
与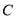 相交于
相交于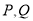 两点,若
两点,若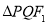 的周长为短轴长的
的周长为短轴长的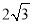 倍.
倍.(1)求
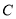 的离心率;
的离心率; (2)设
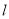 的斜率为
的斜率为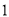 ,在
,在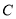 上是否存在一点
上是否存在一点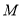 ,使得
,使得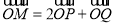 ?若存在,求出点
?若存在,求出点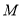 的坐标; 若不存在,说明理由.
的坐标; 若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱柱
 中,底面
中,底面 是菱形,且
是菱形,且 .
.(1) 求证: 平面
 平面
平面 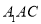 ;
;(2)若
 ,求平面
,求平面 与平面
与平面 所成角的大小.
所成角的大小.
相关试题

