【题目】设函数f(x)满足:
①对任意实数m,n都有f(m+n)+f(m﹣n)=2f(m)f(n);
②对任意m∈R,都有f(1+m)=f(1﹣m)恒成立;
③f(x)不恒为0,且当0<x<1时,f(x)<1.
(1)求f(0),f(1)的值;
(2)判断函数f(x)的奇偶性,并给出你的证明;
(3)定义:“若存在非零常数T,使得对函数g(x)定义域中的任意一个x,均有g(x+T)=g(x),则称g(x)为以T为周期的周期函数”.试证明:函数f(x)为周期函数,并求出 ![]() 的值.
的值.
参考答案:
【答案】
(1)解:由于f(x)不恒为0,故存在x0,使f(x0)≠0,令m=x0,n=0,
则f(x0)+f(0)=2f(x0)f(0),∴f(0)=1,
令m=n=1f(2)+f(0)=2f2(1),
由f(1+m)=f(1﹣m)并令m=1得:f(2)=f(0),
结合以上结果可得f2(1)=1,
又令 ![]() (因为
(因为 ![]() ),
),
∴f(1)<1,故f(1)=﹣1
(2)解:f(x)为偶函数.
证明如下:
令m=0,n=x,得:f(x)+f(﹣x)=2f(0)f(x),以及有f(0)=1,
即有f(﹣x)=f(x),即有f(x)为偶函数
(3)证明:由f(1+m)=f(1﹣m),并取1+m=﹣x,得f(﹣x)=f(2+x),又f(x)为偶函数,
则f(x+2)=f(x),即f(x)是以2为周期的周期函数;
令 ![]() ,
,
再令m= ![]() ,n=
,n= ![]()
![]()
![]() .
.
而 ![]() ,解得,
,解得, ![]() ,
,
由f(1+m)=f(1﹣m)得, ![]() ,
,
∴ ![]() ,
,
又由于f(x)是以2为周期的周期函数,
∴ ![]()
【解析】(1)在等式f(m+n)+f(m﹣n)=2f(m)f(n)中,令m=x0 , n=0,即可求得f(0)=1,结合f(m+n)+f(m﹣n)=2f(m)f(n)、f(1+m)=f(1﹣m)、f(x)不恒为0,且当0<x<1时,f(x)<1即可求得f(1)的值;(2)在f(m+n)+f(m﹣n)=2f(m)f(n)中,取m=0,n=x,以及有f(0)=1,可得函数f(x)为偶函数;(3)由f(1+m)=f(1﹣m),并取1+m=﹣x,得f(﹣x)=f(2+x),又f(x)为偶函数,可得f(x+2)=f(x),即f(x)是以2为周期的周期函数;
在f(m+n)+f(m﹣n)=2f(m)f(n)中,取 ![]() ,取m=
,取m= ![]() ,n=
,n= ![]() 得到两个关于f(
得到两个关于f( ![]() )和f(
)和f( ![]() )的方程组,求出f(
)的方程组,求出f( ![]() )和f(
)和f( ![]() ),再由函数的周期性求得
),再由函数的周期性求得 ![]() 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合M={f(x)|f2(x)﹣f2(y)=f(x+y)f(x﹣y),x,y∈R},有下列命题
①若f(x)= ,则f(x)∈M;
,则f(x)∈M;
②若f(x)=2x,则f(x)∈M;
③f(x)∈M,则y=f(x)的图象关于原点对称;
④f(x)∈M,则对于任意实数x1 , x2(x1≠x2),总有 <0成立;
<0成立;
其中所有正确命题的序号是 . (写出所有正确命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】设定义在R上的奇函数f(x)在(0,+∞)上为增函数,且f(2)=0,则不等式f(x)<0的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC=
 ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣4x+a+3,g(x)=mx+5﹣2m
(1)当a=﹣3,m=0时,求方程f(x)﹣g(x)=0的解;
(2)若方程f(x)=0在[﹣1,1]上有实数根,求实数a的取值范围;
(3)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面上两点A(﹣1,0),B(1,0),在圆C:(x﹣3)2+(y﹣4)2=4上取一点P,
(Ⅰ)x﹣y+c≥0恒成立,求c的范围
(Ⅱ)从x+y+1=0上的点向圆引切线,求切线长的最小值
(Ⅲ)求|PA|2+|PB|2的最值及此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请根据对数函数
 来指出函数
来指出函数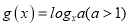 的基本性质(结论不要求证明),并画出图像;
的基本性质(结论不要求证明),并画出图像;(2)拉普拉斯称赞对数是一项“使天文学家寿命倍増”的发明.对数可以将大数之间的乘除运算简化为加减运算,请证明:
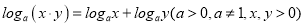 ;
;(3)2017年5月23日至27日,围棋世界冠军柯洁与DeepMind公司开发的程序“AlphaGo”进行三局人机对弈,以复杂的围棋来测试人工智能.围棋复杂度的上限约为
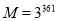 ,而根据有关资料,可观测宇宙中普通物质的原子总数约为
,而根据有关资料,可观测宇宙中普通物质的原子总数约为 .甲、乙两个同学都估算了
.甲、乙两个同学都估算了 的近似值,甲认为是
的近似值,甲认为是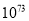 ,乙认为是
,乙认为是 .现有两种定义:
.现有两种定义:
①若实数
 满足
满足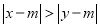 ,则称
,则称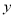 比
比 接近
接近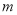 ;
;②若实数
 ,且
,且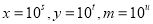 ,满足
,满足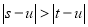 ,则称
,则称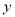 比
比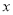 接近
接近 ;请你任选取其中一种定义来判断哪个同学的近似值更接近
;请你任选取其中一种定义来判断哪个同学的近似值更接近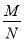 ,并说明理由.
,并说明理由.
相关试题

