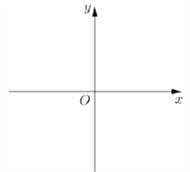
【题目】(1)请根据对数函数![]() 来指出函数
来指出函数![]() 的基本性质(结论不要求证明),并画出图像;
的基本性质(结论不要求证明),并画出图像;
(2)拉普拉斯称赞对数是一项“使天文学家寿命倍増”的发明.对数可以将大数之间的乘除运算简化为加减运算,请证明: ![]() ;
;
(3)2017年5月23日至27日,围棋世界冠军柯洁与DeepMind公司开发的程序“AlphaGo”进行三局人机对弈,以复杂的围棋来测试人工智能.围棋复杂度的上限约为![]() ,而根据有关资料,可观测宇宙中普通物质的原子总数约为
,而根据有关资料,可观测宇宙中普通物质的原子总数约为![]() .甲、乙两个同学都估算了
.甲、乙两个同学都估算了![]() 的近似值,甲认为是
的近似值,甲认为是![]() ,乙认为是
,乙认为是![]() .现有两种定义:
.现有两种定义:
①若实数![]() 满足
满足![]() ,则称
,则称![]() 比
比![]() 接近
接近![]() ;
;
②若实数![]() ,且
,且![]() ,满足
,满足![]() ,则称
,则称![]() 比
比![]() 接近
接近![]() ;请你任选取其中一种定义来判断哪个同学的近似值更接近
;请你任选取其中一种定义来判断哪个同学的近似值更接近![]() ,并说明理由.
,并说明理由.
参考答案:
【答案】(1)见解析;(2) 见解析;(3)见解析.
【解析】试题分析:(1)根据对数函数的性质即可描述函数![]() 的基本性质;
的基本性质;
(2)设![]() ,得
,得![]() ,根据实数指数幂的运算,即可作出证明;
,根据实数指数幂的运算,即可作出证明;
(3)分别采用定义,利用指数幂和对数的运算,即可作出结论.
试题解析:
(1) ![]() ,
,
基本性质为:定义域: ![]() ;值域:
;值域: ![]() ;单调减区间
;单调减区间![]() 和
和![]()
(判断奇偶性、周期性不予给分)
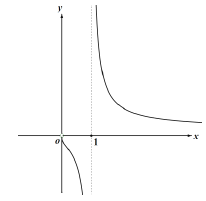
(2)证明: 设![]()
![]()
即![]() 证明完毕
证明完毕
(3)采用定义(Ⅰ): ![]()
![]()
而![]()
![]()
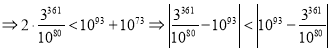
所以甲同学的近似值更接近![]()
采用定义(Ⅱ):
![]()
甲的估值 ![]() ,乙的估值
,乙的估值![]()
因为![]() ,
,
所以乙同学的近似值更接近![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)满足:
①对任意实数m,n都有f(m+n)+f(m﹣n)=2f(m)f(n);
②对任意m∈R,都有f(1+m)=f(1﹣m)恒成立;
③f(x)不恒为0,且当0<x<1时,f(x)<1.
(1)求f(0),f(1)的值;
(2)判断函数f(x)的奇偶性,并给出你的证明;
(3)定义:“若存在非零常数T,使得对函数g(x)定义域中的任意一个x,均有g(x+T)=g(x),则称g(x)为以T为周期的周期函数”.试证明:函数f(x)为周期函数,并求出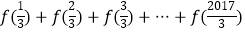 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣4x+a+3,g(x)=mx+5﹣2m
(1)当a=﹣3,m=0时,求方程f(x)﹣g(x)=0的解;
(2)若方程f(x)=0在[﹣1,1]上有实数根,求实数a的取值范围;
(3)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面上两点A(﹣1,0),B(1,0),在圆C:(x﹣3)2+(y﹣4)2=4上取一点P,
(Ⅰ)x﹣y+c≥0恒成立,求c的范围
(Ⅱ)从x+y+1=0上的点向圆引切线,求切线长的最小值
(Ⅲ)求|PA|2+|PB|2的最值及此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆M:
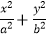 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 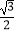 ,直线x=±a和y=±b所围成的矩形ABCD的面积为8.
,直线x=±a和y=±b所围成的矩形ABCD的面积为8.
(Ⅰ)求椭圆M的标准方程;
(Ⅱ)设直线l:y=x+m(m∈R)与椭圆M有两个不同的交点P,Q,l与矩形ABCD有两个不同的交点S,T.求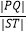 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.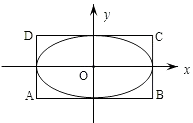
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在(﹣1,1)上的函数f(x)满足:f(x)﹣f(y)=f(
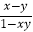 ),当x∈(﹣1,0)时,有f(x)>0;若P=f(
),当x∈(﹣1,0)时,有f(x)>0;若P=f( 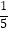 )+f(
)+f( 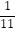 ),Q=f(
),Q=f(  ),R=f(0);则P,Q,R的大小关系为 .
),R=f(0);则P,Q,R的大小关系为 . -
科目: 来源: 题型:
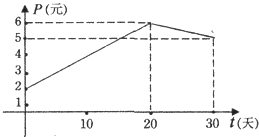
查看答案和解析>>【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示.
第t天
4
10
16
22
Q(万股)
36
30
24
18
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?
相关试题

