【题目】已知![]() 为函数
为函数![]() 图象上一点,
图象上一点, ![]() 为坐标原点,记直线
为坐标原点,记直线![]() 的斜率
的斜率![]() .
.
(1)若函数![]() 在区间
在区间![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求证: ![]()
参考答案:
【答案】(1)实数![]() 的取值范围是
的取值范围是![]() ;(2)实数
;(2)实数![]() 的取值范围是
的取值范围是![]() ;(3)详见解析.
;(3)详见解析.
【解析】试题分析:(1)先利用导数求出函数![]() 的解析式,并利用导数求出函数
的解析式,并利用导数求出函数![]() 的极值点,并将极值点限制在区间
的极值点,并将极值点限制在区间![]() 内,得出有关
内,得出有关![]() 的不等式,求解出实数
的不等式,求解出实数![]() 的取值范围;(2)利用参数分离法将问题
的取值范围;(2)利用参数分离法将问题![]() 在区间
在区间![]() 上恒成立转化为不等式
上恒成立转化为不等式![]() 在区间
在区间![]() 上恒成立,构造新函数
上恒成立,构造新函数![]() ,从而将问题转化为
,从而将问题转化为![]() ,借助导数求函数
,借助导数求函数![]() 的最小值,从而得到实数
的最小值,从而得到实数![]() 的取值范围;(3)取
的取值范围;(3)取![]() ,由(2)中的结论
,由(2)中的结论![]() ,即
,即![]() 在
在![]() 上恒成立,从而得到
上恒成立,从而得到![]() 在
在![]() 上恒成立,,令
上恒成立,,令![]() ,代入上述不等式得到
,代入上述不等式得到![]() ,结合累加法即可证明不等式
,结合累加法即可证明不等式![]() .
.
试题解析:(1)由题意![]() ,
, ![]() 1分
1分
所以![]() 2分
2分
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() 在
在![]() 处取得极大值. 3分
处取得极大值. 3分
因为函数![]() 在区间
在区间![]() (其中
(其中![]() )上存在极值,
)上存在极值,
所以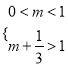 ,得
,得![]() .即实数
.即实数![]() 的取值范围是
的取值范围是![]() . 4分
. 4分
(2)由![]() 得
得![]() ,令
,令![]() ,
,
则![]() . 6分
. 6分
令![]() ,则
,则![]() ,
,
因为![]() 所以
所以![]() ,故
,故![]() 在
在![]() 上单调递增. 7分
上单调递增. 7分
所以![]() ,从而
,从而![]()
![]() 在
在![]() 上单调递增,
上单调递增, ![]()
所以实数![]() 的取值范围是
的取值范围是![]() . 9分
. 9分
(3)由(2) 知![]() 恒成立,
恒成立,
即![]() 11分
11分
令![]() 则
则![]() , 12分
, 12分
所以![]() ,
, ![]() , ,
, , ![]() .
.
将以上![]() 个式子相加得:
个式子相加得: 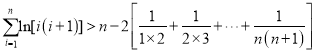
![]() ,
,
故![]() . 14分
. 14分
(解答题的其他解法可酌情给分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.

(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 定义域为
定义域为 ,对任意
,对任意 都有
都有 ,且当
,且当 时,
时,  .
.(1)试判断
 的单调性,并证明;
的单调性,并证明;(2)若
 ,
,①求
 的值;
的值;②求实数
 的取值范围,使得方程
的取值范围,使得方程 有负实数根.
有负实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在直角坐标系xOy中,圆C的参数方程为
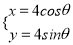 (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为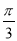 .
.(Ⅰ)写出直线l的参数方程和圆C的标准方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA|·|PB|的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要用甲、乙、丙三辆校车把教职工从老校区接到校本部,已知从老校区到校本部有两条公路,校车走公路①时堵车的概率为
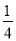 ,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.(1)若三辆校车中恰有一辆校车被堵的概率为
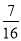 ,求走公路②堵车的概率;
,求走公路②堵车的概率;(2)在(1)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
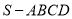 中,底面
中,底面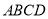 是直角梯形,侧棱
是直角梯形,侧棱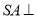 底面
底面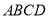 ,
, 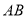 垂直于
垂直于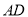 和
和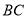 ,
, 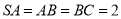 ,
, 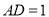 ,
, 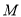 是棱
是棱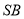 的中点.
的中点.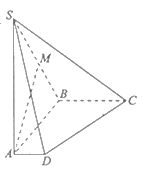
(Ⅰ)求证:
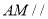 平面
平面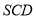 ;
;(Ⅱ)求平面
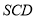 与平面
与平面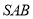 所成的二面角的余弦值;
所成的二面角的余弦值;(Ⅲ)设点
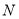 是直线
是直线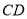 上的动点,
上的动点, 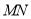 与平面
与平面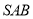 所成的角为
所成的角为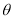 ,求
,求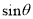 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
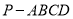 中,底面
中,底面 是平行四边形,
是平行四边形, 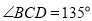 ,侧面
,侧面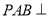 底面
底面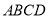 ,
,  ,
, 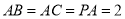 ,
,  分别为
分别为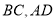 的中点,点
的中点,点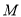 在线段
在线段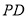 上.
上.(Ⅰ)求证:
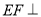 平面
平面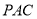 ;
; (Ⅱ)如果直线
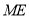 与平面
与平面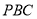 所成的角和直线
所成的角和直线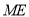 与平面
与平面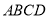 所成的角相等,求
所成的角相等,求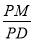 的值.
的值.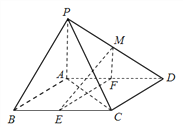
相关试题

