【题目】某学校要用甲、乙、丙三辆校车把教职工从老校区接到校本部,已知从老校区到校本部有两条公路,校车走公路①时堵车的概率为![]() ,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
(1)若三辆校车中恰有一辆校车被堵的概率为![]() ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.
参考答案:
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:
(1)由题意结合概率公式可得三辆校车中恰有一辆校车被堵的概率为![]() ,求走公路②堵车的概率是
,求走公路②堵车的概率是![]() ;
;
(2) 题意可知ξ可能的取值为0,1,2,3,据此计算相应的概率值即可求得分布列,然后可得数学期望为![]() .
.
试题解析:
(1)记“三辆校车中恰有一辆校车被堵”为事件A,由已知条件得事件A发生的概率P(A)= ![]() ×
×![]() ×
×![]() ×(1-p)+(
×(1-p)+( ![]() )2×p=
)2×p=![]() ,
,
解得p=![]() ,
,
所以校车走公路②堵车的概率为![]() .
.
(2)由题意可知ξ可能的取值为0,1,2,3.
P(ξ=0)= ![]() ×
×![]() ×
×![]() =
=![]() ,
,
P(ξ=1)= ![]() ,
,
P(ξ=2)= ![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() ,
,
P(ξ=3)= ![]() ×
×![]() ×
×![]() =
=![]() ,
,
ξ的分布列为
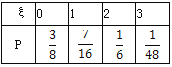
所以Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 定义域为
定义域为 ,对任意
,对任意 都有
都有 ,且当
,且当 时,
时,  .
.(1)试判断
 的单调性,并证明;
的单调性,并证明;(2)若
 ,
,①求
 的值;
的值;②求实数
 的取值范围,使得方程
的取值范围,使得方程 有负实数根.
有负实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在直角坐标系xOy中,圆C的参数方程为
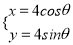 (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为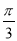 .
.(Ⅰ)写出直线l的参数方程和圆C的标准方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA|·|PB|的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
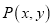 为函数
为函数 图象上一点,
图象上一点,  为坐标原点,记直线
为坐标原点,记直线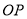 的斜率
的斜率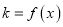 .
.(1)若函数
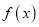 在区间
在区间 上存在极值,求实数
上存在极值,求实数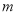 的取值范围;
的取值范围;(2)当
 时,不等式
时,不等式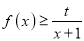 恒成立,求实数
恒成立,求实数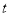 的取值范围;
的取值范围;(3)求证:
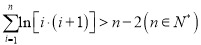
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
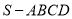 中,底面
中,底面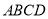 是直角梯形,侧棱
是直角梯形,侧棱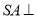 底面
底面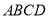 ,
, 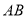 垂直于
垂直于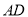 和
和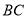 ,
, 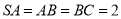 ,
, 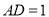 ,
, 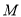 是棱
是棱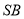 的中点.
的中点.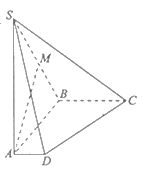
(Ⅰ)求证:
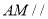 平面
平面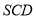 ;
;(Ⅱ)求平面
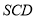 与平面
与平面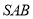 所成的二面角的余弦值;
所成的二面角的余弦值;(Ⅲ)设点
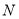 是直线
是直线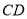 上的动点,
上的动点, 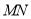 与平面
与平面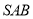 所成的角为
所成的角为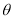 ,求
,求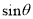 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形, 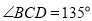 ,侧面
,侧面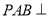 底面
底面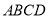 ,
,  ,
, 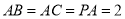 ,
,  分别为
分别为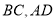 的中点,点
的中点,点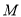 在线段
在线段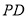 上.
上.(Ⅰ)求证:
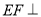 平面
平面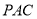 ;
; (Ⅱ)如果直线
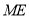 与平面
与平面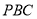 所成的角和直线
所成的角和直线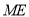 与平面
与平面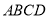 所成的角相等,求
所成的角相等,求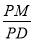 的值.
的值.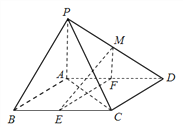
-
科目: 来源: 题型:
查看答案和解析>>【题目】信息科技的进步和互联网商业模式的兴起,全方位地改变了大家金融消费的习惯和金融交易模式,现在银行的大部分业务都可以通过智能终端设备完成,多家银行职员人数在悄然减少.某银行现有职员320人,平均每人每年可创利20万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.2万元,但银行需付下岗职员每人每年6万元的生活费,并且该银行正常运转所需人数不得小于现有职员的
 ,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
相关试题

