【题目】已知![]() 定义域为
定义域为![]() ,对任意
,对任意![]() 都有
都有![]() ,且当
,且当![]() 时,
时, ![]() .
.
(1)试判断![]() 的单调性,并证明;
的单调性,并证明;
(2)若![]() ,
,
①求![]() 的值;
的值;
②求实数![]() 的取值范围,使得方程
的取值范围,使得方程![]() 有负实数根.
有负实数根.
参考答案:
【答案】(1) ![]() 是
是![]() 上的减函数; (2)①
上的减函数; (2)①![]() ; ②
; ②![]() 的取值范围
的取值范围![]()
【解析】试题分析:(1)利用定义证明:任取![]() ,且
,且![]() ,
,
![]()
![]() ,
, ![]() ,
, ![]() 下结论(2)①先赋值
下结论(2)①先赋值![]()
求得![]() ,再令
,再令![]() 可解得
可解得![]() ②方程
②方程![]() 可化为
可化为![]() ,又
,又![]() 单调,所以只需
单调,所以只需![]() 有负实数根.对
有负实数根.对![]() 进行分类讨论,分
进行分类讨论,分![]() 与
与![]() 两种情况.
两种情况.
试题解析:
解:(1)任取![]() ,且
,且![]() ,
,
![]()
![]() ,
, ![]() ,
, ![]() 是
是![]() 上的减函数;
上的减函数;
(2)①![]() ,
, ![]() ,
,
又![]() ,因为
,因为![]() ,
,
![]() ,
,
②方程![]() 可化为
可化为![]() ,又
,又![]() 单调,所以只需
单调,所以只需![]() 有负实数根.记
有负实数根.记![]() ,
,
当![]() 时,
时, ![]() ,解得
,解得![]() ,满足条件;
,满足条件;
当![]() 时,函数
时,函数![]() 图像是抛物线,且与
图像是抛物线,且与![]() 轴的交点为(0,-1),方程
轴的交点为(0,-1),方程![]() 有负实根包含两类情形:
有负实根包含两类情形:
①两根异号,即![]() ,解得
,解得![]() ;
;
②两个负实数根,即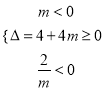 ,解得
,解得![]() .
.
综上可得,实数![]() 的取值范围
的取值范围![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图:
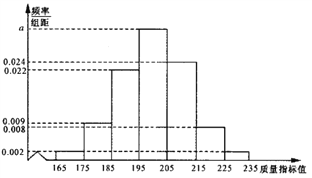
(Ⅰ)求直方图中
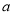 的值;
的值;(Ⅱ)由频率分布直方图可以认为,这种产品的质量指标值
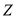 服从正态分布
服从正态分布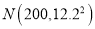 ,试计算数据落在
,试计算数据落在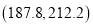 上的概率.
上的概率.参考数据:若
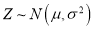 ,则
,则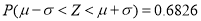 ,
, 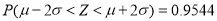 .
.(Ⅲ)设生产成本为
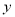 ,质量指标为
,质量指标为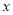 ,生产成本与质量指标之间满足函数关系
,生产成本与质量指标之间满足函数关系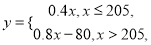 假设同组中的每个数据用该组区间的右端点值代替,试计算生产该食品的平均成本.
假设同组中的每个数据用该组区间的右端点值代替,试计算生产该食品的平均成本. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
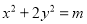 (
(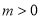 ),以椭圆内一点
),以椭圆内一点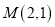 为中点作弦
为中点作弦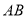 ,设线段
,设线段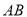 的中垂线与椭圆相交于
的中垂线与椭圆相交于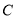 ,
, 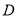 两点.
两点.(Ⅰ)求椭圆的离心率;
(Ⅱ)试判断是否存在这样的
 ,使得
,使得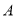 ,
, 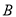 ,
, 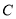 ,
, 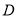 在同一个圆上,并说明理由.
在同一个圆上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.

(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在直角坐标系xOy中,圆C的参数方程为
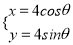 (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为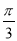 .
.(Ⅰ)写出直线l的参数方程和圆C的标准方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA|·|PB|的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
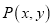 为函数
为函数 图象上一点,
图象上一点,  为坐标原点,记直线
为坐标原点,记直线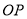 的斜率
的斜率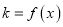 .
.(1)若函数
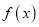 在区间
在区间 上存在极值,求实数
上存在极值,求实数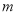 的取值范围;
的取值范围;(2)当
 时,不等式
时,不等式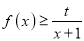 恒成立,求实数
恒成立,求实数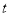 的取值范围;
的取值范围;(3)求证:
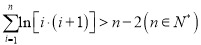
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要用甲、乙、丙三辆校车把教职工从老校区接到校本部,已知从老校区到校本部有两条公路,校车走公路①时堵车的概率为
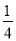 ,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.
,校车走公路②时堵车的概率为p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆校车是否堵车相互之间没有影响.(1)若三辆校车中恰有一辆校车被堵的概率为
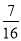 ,求走公路②堵车的概率;
,求走公路②堵车的概率;(2)在(1)的条件下,求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.
相关试题

