搜索
【题目】已知圆C：x2+y2=4，点P为直线x+2y﹣9=0上一动点，过点P向圆C引两条切线PA、PB，A、B为切点，则直线AB经过定点（ ）
A.
B.
C.（2，0）
D.（9，0）
参考答案：
【答案】A
【解析】解：因为P是直线x+2y﹣9=0的任一点，所以设P（9﹣2m，m）， 因为圆x2+y2=4的两条切线PA、PB，切点分别为A、B，
所以OA⊥PA，OB⊥PB，
则点A、B在以OP为直径的圆上，即AB是圆O和圆C的公共弦，
则圆心C的坐标是（ 
， 
），且半径的平方是r2= 
，
所以圆C的方程是（x﹣ ）2+（y﹣ ）2= ，①
又x2+y2=4，②，
②﹣①得，（2m﹣9）x﹣my+4=0，即公共弦AB所在的直线方程是：（2m﹣9）x﹣my+4=0，
即m（2x﹣y）+（﹣9x+4）=0，
由 
得x= 
，y= 
，
所以直线AB恒过定点（ ， ），
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在等差数列{an}中，a2=6，a3+a6=27．
（1）求数列{an}的通项公式；
（2）若数列{bn}的通项公式为
，求数列{anbn}的前n项的和Tn ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四棱锥
，底面
为菱形， 
平面
， 
， 
分别是
的中点．（Ⅰ）证明：
；（Ⅱ）若
为
上的动点， 
与平面
所成最大角的正切值为
，求二面角
的余弦值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
的最小正周期为π．
（1）求ω的值；
（2）讨论f（x）在区间
上的单调性． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知动点 P 与定点
的距离和它到定直线 x 4 的距离的比是1: 2 ，记动点 P 的轨迹为曲线 E．（1）求曲线 E 的方程；
（2）设 A 是曲线 E 上的一个点，直线 AF 交曲线 E 于另一点 B，以 AB 为边作一个平行四边形，顶点 A、B、C、D 都在轨迹 E 上，判断平行四边形 ABCD 能否为菱形，并说明理由；
（3）当平行四边形 ABCD 的面积取到最大值时，判断它的形状，并求出其最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】给出以下命题：
（1）若
：
；
：
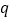，则
为真，
为假，
为真（2）“
”是“曲线
表示椭圆”的充要条件（3）命题“若
，则
”的否命题为：“若，则
”（4）如果将一组数据中的每一个数都加上同一个非零常数，那么这组数据的平均数和方差都改变；
则正确命题有（ ）个
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x﹣
，g（x）=x2﹣2ax+4，若任意x1∈[0，1]，存在x2∈[1，2]，使f（x1）≥g（x2），求实数a的取值范围．
相关试题
