【题目】已知函数f(x)=x﹣ ![]() ,g(x)=x2﹣2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),求实数a的取值范围.
,g(x)=x2﹣2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),求实数a的取值范围.
参考答案:
【答案】解:由于f′(x)=1+ ![]() >0,因此函数f(x)在[0,1]上单调递增,
>0,因此函数f(x)在[0,1]上单调递增,
所以x∈[0,1]时,f(x)min=f(0)=﹣1.
根据题意可知存在x∈[1,2],
使得g(x)=x2﹣2ax+4≤﹣1,即x2﹣2ax+5≤0,即a≥ ![]() 能成立,
能成立,
令h(x)= ![]() ,则要使a≥h(x)在x∈[1,2]能成立,只需使a≥h(x)min ,
,则要使a≥h(x)在x∈[1,2]能成立,只需使a≥h(x)min ,
又函数h(x)= ![]() 在x∈[1,2]上单调递减,
在x∈[1,2]上单调递减,
所以h(x)min=h(2)= ![]() ,故只需a≥
,故只需a≥ ![]()
【解析】若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),即存在x∈[1,2],使得g(x)=x2﹣2ax+4≤﹣1,即x2﹣2ax+5≤0,解得实数a的取值范围.
【考点精析】本题主要考查了二次函数的性质和利用导数研究函数的单调性的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间
上递减;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2=4,点P为直线x+2y﹣9=0上一动点,过点P向圆C引两条切线PA、PB,A、B为切点,则直线AB经过定点( )
A.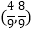
B.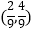
C.(2,0)
D.(9,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点 P 与定点
 的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.(1)求曲线 E 的方程;
(2)设 A 是曲线 E 上的一个点,直线 AF 交曲线 E 于另一点 B,以 AB 为边作一个平行四边形,顶点 A、B、C、D 都在轨迹 E 上,判断平行四边形 ABCD 能否为菱形,并说明理由;
(3)当平行四边形 ABCD 的面积取到最大值时,判断它的形状,并求出其最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下命题:
(1)若
 :
: ;
;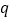 :
: ,则
,则 为真,
为真, 为假,
为假, 为真
为真(2)“
 ”是“曲线
”是“曲线 表示椭圆”的充要条件
表示椭圆”的充要条件(3)命题“若
 ,则
,则 ”的否命题为:“若
”的否命题为:“若 ,则
,则 ”
”(4)如果将一组数据中的每一个数都加上同一个非零常数,那么这组数据的平均数和方差都改变;
则正确命题有( )个
A.
 B.
B.  C.
C.  D.
D. 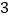
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 ABC中,角A,B,C的对边分别是a,b,c,已知2acosA=-
ABC中,角A,B,C的对边分别是a,b,c,已知2acosA=-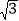 (ccosB+bcosC)。
(ccosB+bcosC)。(1)求角A;
(2)若b=2,且
 ABC的面积为
ABC的面积为 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据所给的条件求直线的方程:
(1)直线过点(-4,0),倾斜角的正弦值为
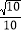 ;
;(2)直线过点(5,10),到原点的距离为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
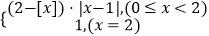 ,其中[x]表示不超过x的最大整数.设n∈N* , 定义函数fn(x):f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn﹣1(x))(n≥2),则下列说法正确的有 ①y=
,其中[x]表示不超过x的最大整数.设n∈N* , 定义函数fn(x):f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn﹣1(x))(n≥2),则下列说法正确的有 ①y= 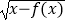 的定义域为
的定义域为 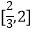 ;
;
②设A={0,1,2},B={x|f3(x)=x,x∈A},则A=B;
③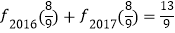 ;
;
④若集合M={x|f12(x)=x,x∈[0,2]},
则M中至少含有8个元素.( )
A.1个
B.2个
C.3个
D.4个
相关试题

