搜索
【题目】在等差数列{an}中，a2=6，a3+a6=27．
（1）求数列{an}的通项公式；
（2）若数列{bn}的通项公式为 
，求数列{anbn}的前n项的和Tn ．
参考答案：
【答案】
（1）解：设等差数列{an}的公差为d，则an=a1+（n﹣1）d．
由a2=6，a3+a6=27，可得 
解得 
．
从而，an=3n
（2）解：由（1）可知an=3n，
∴ 
． 
①
②
①﹣②，得： 
故 
【解析】（1）利用等差数列的通项公式即可得出．（2）由（1）可知 ．利用“错位相减法”与等比数列的求和公式即可得出．
【考点精析】关于本题考查的等差数列的通项公式（及其变式）和数列的前n项和，需要了解通项公式：
或
；数列{an}的前n项和sn与通项an的关系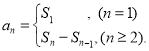
才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】从一批柚子中，随机抽取100个，获得其重量（单位：克）数据按照区间
，
，
，
进行分组，得到概率分布直方图，如图所示.（1）根据频率分布直方图计算抽取的100个柚子的重量众数的估计值.
（2）用分层抽样的方法从重量在
和的柚子中共抽取5个，其中重量在的有几个？（3）在（2）中抽出的5个柚子中，任取2人，求重量在
的柚子最多有1个的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知公差不为0的等差数列{an}的首项a1为a(a∈R)．设数列的前n项和为Sn，且
，
，
成等比数列．(1)求数列{an}的通项公式及Sn；
(2)记
，
.当n≥2时，求An与Bn． -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=x﹣a（x+1）ln（x+1），（x＞﹣1，a≥0）
（Ⅰ）求f（x）的单调区间；
（Ⅱ）当a=1时，若方程f（x）=t在
上有两个实数解，求实数t的取值范围；
（Ⅲ）证明：当m＞n＞0时，（1+m）n＜（1+n）m ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四棱锥
，底面
为菱形， 
平面
， 
， 
分别是
的中点．（Ⅰ）证明：
；（Ⅱ）若
为
上的动点， 
与平面
所成最大角的正切值为
，求二面角
的余弦值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
的最小正周期为π．
（1）求ω的值；
（2）讨论f（x）在区间
上的单调性． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆C：x2+y2=4，点P为直线x+2y﹣9=0上一动点，过点P向圆C引两条切线PA、PB，A、B为切点，则直线AB经过定点（ ）
A.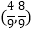
B.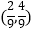
C.（2，0）
D.（9，0）
相关试题
